Funktor
Från Rilpedia
Inom kategoriteorin i matematik är en funktor en tillordning som på ett naturligt sätt till varje objekt i en kategori associerar ett annat objekt.
Inledning
En mycket vanlig konstruktion i matematiken är att man till en strukur av en viss typ associerar en annan struktur. Några exempel på sådana konstruktioner är:
- Till ett topologiskt rum associerar man dess homologigrupper
- Till en ring associerar man dess maximala fraktionsring
- Till en grupp associerar man dess centrum
- Till ett komplex associerar man dess homologikomplex
- Givet en abelsk grupp N, associerar man till varje abelsk grupp gruppen av homomorfier Hom(M,N)
Om en sådan association är sådan att avbildningar mellan två strukturer på ett naturligt sätt inducerar avbildningar mellan de associerade strukurererna, kallas associationen för en funktor. Mer allmänt kan man definiera funktorer mellan två kategorier Alla associationer i listan ovan är funktorer.
Definition
Givet två kategorier C,D, så är en (kovariant) funktor F ett par av tillordningar (F0,F1) där F0 avbildar objekt i C på objekt i D och F1 avbildar morfier i C på morfier i D sådan att följande är sant:
- Om
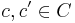 och
och 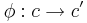 så gäller
så gäller 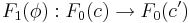
- Om
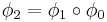 så
så 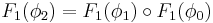
För en kontravariant funktor ersätts det första villkoret med:
- Om
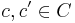 och
och 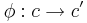 så gäller
så gäller 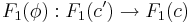
Kovariant och kontravariant funktor
En kovariant funktor är en funktor som bevarar ordningen på morfierna.
En kontravariant funktor är en funktor som kastar om ordningen på morfierna.



