Diofantisk ekvation

Från Rilpedia

Texten från svenska Wikipedia

Diofantiska ekvationer har fått sitt namn av den grekiske matematikern Diofantos som var verksam under mitten av 200-talet och studerade denna typ av ekvationer. Det som utmärker en diofantisk ekvation är inte dess utseende utan att de endast tillåter heltalslösningar. Alla ekvationer kan således ses som diofantiska ekvationer och skillnaden blir att endast de lösningar som tillhör de hela talen godtags. De diofantiska ekvationerna är vanligtvis (men inte nödvändigtvis) polynom ekvationer med heltalskoefficienter av godtycklig grad med ett godyckligt antal variabler. Då alla variabler har samma grad i en diofantisk ekvation kallas den för homogen. Man skiljer oftast på de linjära och icke-linjära diofantiska ekvationerna.

Innehåll

1 Lösningar till diofantiska ekvationer
2 Linjära diofantiska ekvationer
3 Icke-linjära diofantiska ekvationer
- 3.1 Kända diofantiska ekvationer
4 Referenser

Lösningar till diofantiska ekvationer

Eftersom att diofantiska ekvationer endast tillåter heltals lösningar leder detta till att många ekvationer blir omöjliga att lösa. Beroende på ekvationens utseende, antalet variabler och grad, kan en diofantisk ekvationen ha allt ifrån noll till oändligt antal lösningar. Ett utav David Hilberts tjugotre problem handlar om diofantiska ekvationer (problem nummer 10). Frågan som ställs är om det finns en algoritm som kan användas för att bestämma om en given polynomiell diofantisk ekvation med heltalskofficienter har en heltalslösning. Svaret på frågan är "Nej" och bevisas av Matiyasevichs. Det finns även andra intressanta sats bl.a. Thues sats ,efter Axel Thue, säger att en homogen diofantisk ekvation med grad större än 3 har ett ändligt antal lösningar.

Linjära diofantiska ekvationer

Linjära diofantiska ekvationer är polynom ekvationer på formen $a 1 x 1 + a 2 x 2 + ... + a n x n = b$ där $a 1,..., a n$ och $b$ är konstanter, och $x 1,..., x n$ är variabler.

En variabel

I en variabel har en diofantisk ekvation formen $a x = b$ , ekvationen har endast lösning då $a$ delar $b$ dvs. $x = a / b$ där $a / b$ tillhör de hela talen.

Två variabler

I två variabler har ekvationen utseendet $a x + b y = c$ . Vi har då följande sats.

Om $(x 0, y 0)$ är en lösning till den diofantiska ekvationen $a x + b y = c$ där $a, b, c$ tillhör de hela talen fås alla lösningar av.

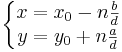$\left\{\begin{matrix} x=x_0-n \frac{b}{d} \\ y=y_0+n \frac{a}{d} \end{matrix}\right.$ , där $d = S G D (a, b)$ och $n$ är ett godtyckligt heltal.

Detta bevisas på följande vis. Anta att $(x, y)$ och $(x 0, y 0)$ är lösningar till $a x + b y = c$ , vi får då att.

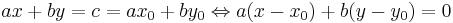
$ax+by=c=ax_0+by_0 \Leftrightarrow a(x-x_0)+b(y-y_0)=0$

Division med $d$ ger att
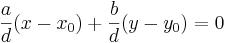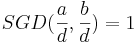
$\frac{a}{d}(x-x_0)+\frac{b}{d}(y-y_0)=0$ , där $SGD(\frac{a}{d},\frac{b}{d})=1$

Det följer då att $a / d$ delar $(y - y 0)$ som ger att
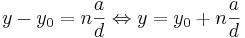
$y-y_0=n\frac{a}{d} \Leftrightarrow y=y_0+n\frac{a}{d}$

Använding av ovanstående resultat ger att.

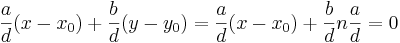
$\frac{a}{d}(x-x_0)+\frac{b}{d}(y-y_0)=\frac{a}{d}(x-x_0)+\frac{b}{d}n\frac{a}{d}=0$

Som i sin tur ger att.

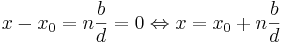
$x-x_0=n\frac{b}{d}=0 \Leftrightarrow x=x_0+n\frac{b}{d}$

Vilket bevisar att alla lösningar till den diofantiska ekvationen $a x + b y = c$ där $a, b, c$ tillhör de hela talen ges av.

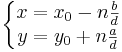$\left\{\begin{matrix} x=x_0-n \frac{b}{d} \\ y=y_0+n \frac{a}{d} \end{matrix}\right.$ , där $(x 0, y 0)$ är en lösning till den diofantiska ekvationen, $d = S G D (a, b)$ och $n$ är ett godtyckligt heltal.

Ovanstående metod ger alla lösningar till en linjär diofantisk ekvation i två variabler men den förutsätter att en lösningen är given/funnen. Ibland är det lätt att hitta en lösning ibland svårare, för att finna en lösning kan man bland annat använda Euklides algoritm.

Euklides algoritm

Euklides algoritm beskrivs bäst med hjälp av ett exempel. Anta att vi vill lösa den diofantiska ekvationen $97 x + 35 y = 13$ . Vi använder då Euklides algoritm för att finns $S G D (97,35)$

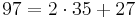
$97=2\cdot35+27$

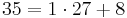
$35=1\cdot27+8$

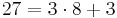
$27=3\cdot8+3$

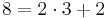
$8=2\cdot3+2$

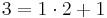
$3=1\cdot2+1$

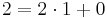
$2=2\cdot1+0$

Alltså är $S G D (97,35) = 1$ , nu använda ovanstående resultat för att skriva $S G D (97,35)$ som en linjär kombination av 97 och 35.

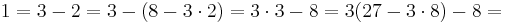
$1=3-2=3-(8-3\cdot2)=3\cdot3-8=3(27-3\cdot8)-8=$
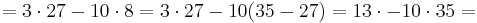
$=3\cdot27-10\cdot8=3\cdot27-10(35-27)=13\cdot-10\cdot35=$
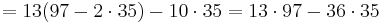
$=13(97-2\cdot35)-10\cdot35=13\cdot97-36\cdot35$

Vilket ger oss följande uttryck.

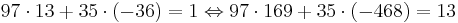
$97\cdot13+35\cdot(-36)=1 \Leftrightarrow 97\cdot169+35\cdot(-468)=13$

En lösning till vår diofantiska ekvation är således $x = 169, y = - 468$ .

Tre eller fler variabler

I tre eller fler variabler har ekvationen utseendet $a 1 x 1 + a 2 x 2 + a 3 x 3 + ... + a n x n = c$ . I två variabler gällde att den diofantiska ekvationen endast hade en eller flera lösningar om största gemensamma delaren för kofficienterna framför variblerna delade högerledet. För tre eller flera variabler kan liknande slutsatser dras.

Icke-linjära diofantiska ekvationer

Skillnanden mellan de linjära och icke-linjära diofnatiska ekvationerna är att de icke-linjära har variabler med grad högre än 1 och kan dessutom innehålla produkter av två eller fler av de ingående variablerna.

Kända diofantiska ekvationer

Genom historien har ett antal diofantiska ekvationer uppkommit och vissa har blivit mer kända än andra. Nedan följernågra välkända diofantiska ekvationer.

Pythagoras sats

$a 2 + b 2 = c 2$ och dess heltalslösningar utgör sidorna i en triangel och kallas ofta för pythagoras triplar.
Den mest kända är för $a = 3$ , $b = 4$ , $c = 5$ och kallas för den egyptiska triangeln.

Fermats stora sats

$x n + y n = z n$ för $n > 2$ saknar lösningar och kallas för Fermats stora sats efter den franske 1600-tals matematikern Pierre de Fermat.
Det tog över 350 år för världens matematiker att bevisa satsen.

Pell's ekvation

$x 2 - n y 2 = 1$ där $n$ är ett heltal men ej en kvadrat av ett annat tal och kallas för Pell's ekvation efter den engelske matematikern John Pell.
Exempel: $x 2 - 5 y 2 = 1$ löses t.ex. av $x = 9$ , $y = 4$ .

Referenser

L.J. Mordell (1969). Diophantine equations. Academic Press. ISBN 0125062508.
H. Cohen (2007). Number theory. Vol. 1, Tools and diophantine equations. Springer. ISBN 0387499229.

Diofantisk ekvation

Från Rilpedia

Innehåll

Lösningar till diofantiska ekvationer

Linjära diofantiska ekvationer

En variabel

Två variabler

Euklides algoritm

Tre eller fler variabler

Icke-linjära diofantiska ekvationer

Kända diofantiska ekvationer

Pythagoras sats

Fermats stora sats

Pell's ekvation

Referenser

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk