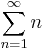Aritmetisk serie
Från Rilpedia
Aritmetisk serie, används i viss litteratur och dylikt då antingen aritmetiska följder eller artimetiska summor åsyftas (se definitioner nedan).
Ordet aritmetisk serie är dock närmast motsägelsefullt eftersom en serie inom matematiken är "en summa av uppräkneligt oändligt antal termer". Utifall att en sådan oändlig summa även vore aritmetisk så skulle den oundvikligen divergera (gå mot oändligheten) och därmed vara långt mindre intressant. Man kan dock få fram finita värden för vissa sådana serier med hjälp av analytiska fortsättningar.
Man bör således undvika ordet aritmetisk serie och istället använda antingen:
- Aritmetisk följd, en följd av tal där skillnaden mellan på varandra följande tal är konstant.
- Exempel:
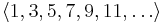
- Exempel:
- Aritmetisk summa, en summa där skillnaden av på varandra följande termer är konstant.
- Exempel:
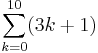
- Exempel:
Summan av alla positiva heltal
Summan av alla positiva heltal,
är uppenbart divergent. Med hjälp av analytiska fortsättningar och Riemanns zetafunktion kan man dock evaluera den till $-1/12$, vilken bland annat används i strängteori.