B (mjukvaruutveckling)
Från Rilpedia
B är en mjukvaruutvecklingsmetod framtagen av Jean-Raymond Abrial, tillika ett språk och CASE-verktyg från B-Core (UK) Ltd..
B-metoden är nästan unik bland formella mjukvaruutvecklingsmetoder i det avseendet att den använder samma notation för specifikation, design och programmeringen.
Språket B byggs upp med hjälp av matematiska formler med vars hjälp det går att validera programmet. På detta sättet går det att ta fram matematiska bevis att programmet fungera innan det riktiga programmet skrivs.
Innehåll |
Exempel på notation
| Matematik | motsvarighet i B | Beskrivning |
|---|---|---|
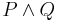 |
P & Q | Konjunktion |
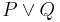 |
P or Q | Disjunktion |
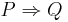 |
P=>Q | Implikation |
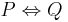 |
P<=>Q | Ekvivalens |
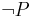 |
not P | Negation |
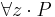 |
!(z).P | Allkvantifikator |
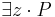 |
#(z).P | Existenskvantifikator |
![\left[ G \right] P](/w/images/sv.rilpedia.org/math/4/2/5/42581257ef0895afce46b08cddd35b16.png) |
[G]P | substitution |
Exempel på Substitutioner
Kompilatorn i B omvandlar språkets olika element i matematiska formler. Nedan följer exempel på några sådana Substitutioner
| Psedu-program | Regel | Beskrivning |
|---|---|---|
| [BEGIN G END] Q | ![\left[ G \right] Q](/w/images/sv.rilpedia.org/math/9/d/d/9dd4add936630b5957ab175c5468654d.png) |
Villkor Q måste uppfyllas medan G execueras. |
| [PRE P THEN G END] Q | ![P \wedge \left[ G \right] Q](/w/images/sv.rilpedia.org/math/b/e/a/bea8faa1e6e28f4841ede22a3cfd527d.png) |
Innan programmet G execuerats måste villkoret P uppfyllas och villkoret Q måste uppfyllas under hela execueringen. |
| [IF P THEN G ELSE H END] Q | ![\left(P \Rightarrow \left[ G \right] Q \right) \wedge \left( \neg P \Rightarrow \left[ H \right] Q \right)](/w/images/sv.rilpedia.org/math/1/7/b/17bcfc910283b7579d4c1bc6bba2331a.png) |
Om villkoret P uppfylls execueras kod G, annars H. Oavsett vilken kod som execueras måste villkor Q uppfyllas hela tiden. |
| [G ; WHILE P DO H VARIANT E INVARIANT I END] Q |
![\left( \left[ G \right] I \right) \wedge](/w/images/sv.rilpedia.org/math/5/c/a/5cadd06a439a3595339640ecf6ccfbee.png)
|
Efter att kod G execuerats execureras kod H så länge villkor P uppfylls. Loopvariabel är E och under hela tiden måste villkor I uppfyllas. |
Exempel på program i B
Detta program definierar en maskin Positive som representera ett naturligt tal mellan 0 och maxint med startvärde 0. Till maskinen finns operationerna set (för att ändra värde), read (för att läsa värde) och incr (för att öka med ett).
MACHINE Positive (maxint) VARIABLES val INVARIANT val0 .. maxint INITIALISATION val := 0 OPERATIONS set (xx) = PRE xx
0 .. maxint THEN val := xx END ; vv ← read = vv := val ; incr = PRE val < maxint THEN val := val + 1 END ; END
Det som mest skiljer detta programmet från vanliga program är INVARIANT som måste uppfyllas under hela programmets gång och PRE som måste uppfyllas vid execuering. Om det finns någon matematisk sannolikhet att dessa villkor inte uppfylls någon gång under programmets gång misslyckas kompileringen. På så sätt går det att redan under kompileringen få reda på om det finns någon bugg i programmet som annars kanske skulle ha upptäckts först efter att ha kört programmet under lång tid.
Böcker
- [Wordsworth, J.B. ] (1996) Software Engineering with B, ISBN 0-201-40356-0




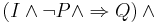
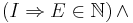
![\left( I \wedge P \Rightarrow \left[ y:= E \right] \left[ H \right] E < y \right) \wedge](/w/images/sv.rilpedia.org/math/4/8/1/481f23fcede4c43ea00178781a48ca1c.png)
![\left( I \wedge P \Rightarrow \left[ H \right] I \right)](/w/images/sv.rilpedia.org/math/7/e/d/7ed9a270cbfc8d0bebb122f0ac988366.png)