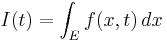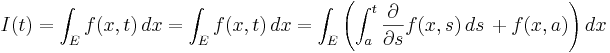Derivering av integraler
Från Rilpedia
Version från den 16 maj 2009 kl. 17.47 av Petter Strandmark (Diskussion)
Derivering av integraler är en central operation i matematisk analys. Det är ofta relevant att fråga huruvida funktioner av typen
har någon derivata och i så fall vilken.
Innehåll |
Derivering genom byte av integrationsordning
Under vissa förutsättningar (se byte av integrationsordning) kan dessa integraler beräknas i omvänd ordning och 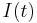 blir då lika med.
blir då lika med.
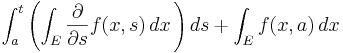 ,
,
varvid
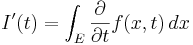 .
.
Tillräckliga krav
Dessa krav är var för sig tillräckliga för att det skall vara tillåtet att flytta deriveringen innanför integralen:
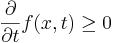 för alla
för alla 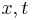
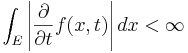
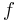 och
och 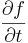 är begränsade och kontinuerliga i
är begränsade och kontinuerliga i 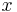 och
och 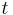
Exempel
Betrakta funktionen
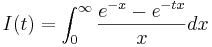 .
.
Vi ser direkt att 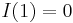 och att
och att
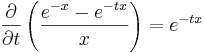 .
.
Eftersom derivatan alltid är positiv kan vi byta integrationsordning:
![I(t) = \int_0^\infty \left( \int_1^t e^{-sx} ds \right) dx = \int_1^t \left( \int_0^\infty e^{-sx} dx \right) ds = \int_1^t \left[ \frac{e^{-sx}}{-s}\right]_{x=0}^{x=\infty} ds = \int_1^t \frac{1}{s} ds = \log t](/w/images/sv.rilpedia.org/math/9/6/0/960a1c6273a25317829689e277df88da.png) .
.
Genom att derivera var det alltså möjligt att beräkna 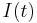 explicit.
explicit.
Referenser
- G. B. Folland, Real Analysis: Modern Techniques and Their Applications, John Wiley and Sons 1999 ISBN 0-471-317160-0