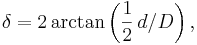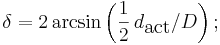Vinkeldiameter

Från Rilpedia

Version från den 27 mars 2009 kl. 10.40 av Alexbot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Vinkeldiametern hos ett objekt sett från en observatör är den "visuella diametern" hos objektet mätt som en vinkel. Inom astronomin är storleken på objekt i stjärnhimmeln ofta uttryckta i form av dess vinkeldiameter sett från jorden, snarare än deras faktiska storlek. Vinkeldiametern hos jordens bana runt solen, sedd från ett avstånd av en parsec, är 2" (två bågsekunder). Från en observatör på ett avstånd av ett ljusår har solen en vinkeldiameter på 0,03" och jorden 0,0003".

Beräkning

Vinkeldiametern hos ett objekt kan beräknas genom följande formel:

\delta = 2 \arctan \left( \frac{1}{2}\,d / D \right),

där δ är vinkeldiametern, d och D är den visuella diametern och avståndet till objektet, uttryckta i samma enheter. När D är mycket större än d kan δ approximeras av δ = d / D där resultatet fås i radianer.

För ett sfäriskt objekt vars verkliga diameter är lika med dact, kan vinkeldiametern fås genom formeln:

\delta = 2 \arcsin \left( \frac{1}{2}\,d_\mbox{act} / D \right);

I praktiska sammanhang är skillnaden mellan d och dact bara avgörande för sfäriska objekt som befinner sig relativt nära observatören.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Vinkeldiameter"
Personliga verktyg