Snedprojektion
Från Rilpedia
Snedprojektion är en enkel typ av grafisk projektion som används för att skapa tvådimensionella bilder av tredimensionella föremål.
Innehåll |
Definition och metod
Snedprojektion är en sorts parallellprojektion. Den projicerar med hjälp av parallella strålar ("projektionsstrålar") det tredimensionella föremålet på ritytan ("projektionsplanet"). I både snedprojektion och ortografisk projektion (den andra typen av "parallell projektion") skapas avbildningen genom parallella strålar från objektet. Projektionsstrålarna skär projektionsplanet i snedprojektion i en sned vinkel för att så skapa bilden, i motsats till den perpendikulära vinkeln som används i ortografisk projektion.
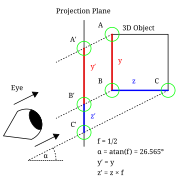
Matematiskt sett ger parallellprojektionen av punkten (x,y,z) på xy-planet (x + az,y + bz,0). Konstanterna a och b beskriver en entydig parallellprojektion. När a = b = 0, kallas projektionen ortografisk eller ortogonal. I annat fall är den "sned".
Konstanterna a och b är inte nödvändigtvis mindre än 1, och som en konsekvens kan längder som mäts i en snedprojektion vara antingen längre eller kortare än de är i rummet. I en allmän snedprojektion avbildas sfärer i rummet som ellipser på projektionsplanet, och inte som cirklar som man skulle förvänta sig av en ortogonal projektion.
Snedprojektion är också den grövsta tredimensionella projektionsmetoden men också den enklaste att behärska. Snedprojektion är inte en verklig tredimensionell avbildning utan bara en tvådimensionell bild av föremålet med ett "påtvingat djup". Ett sätt att rita och använda snedprojektion är att rita den sida av föremålet man betraktar i två dimensioner, dvs en platt avbildning, och sedan rita den andra sidan i en vinkel av 45 grader, men i stället för att rita sidan i full storlek ritas den bara i halv längd (djup) och skapar det påtvingade djupet, och lägger ett drag av realism till föremålet. Även med detta "påtvingade djup" ger snedprojektion inte en för ögat övertygande bild. Av detta skäl används den sällan av professionella designers och ingenjörer.
Sned avbildning
I en teckning med snedprojektion är vinklarna mellan koordinataxlarna, såväl som skalningsfaktorn längs axlarna, godtyckliga. Mer exakt, varje given uppsättning av tre sammanfallande plansegment som utgår från samma punkt kan avbilda tre sidor av en kub. Detta är känt som Pohlkes teorem, efter den tyske matematikern Pohlke, som publicerade resultatet i början av 1900-talet.[1]
De resulterande distorsionerna gör tekniken olämplig för formella arbetsritningar. Hur som helst, distorsionen kan minskas genom att lägga ett plan i bilden parallellt med projektionsplanet. Gör man så får man en sann avbildning längs det valda planet. Denna speciella form av snedprojektion, där längder längs x-axeln och y-axeln bevaras, men längder längs z-riktningen ritas i vinkel och med en reduktionsfaktor används mycket för industriella ritningar.
Kavaljersperspektiv är namnet på en sådan projektion, där längden längs "z"-axeln förblir oskalad.[2]
Kabinettprojektion, populär för möbelillustrationer, är ett exempel på en sådan teknik, där den försvinnande axeln är skalad till halv skala. [2]
Exempel
Förutom för tekniska ritningar och illustrationer används snedprojektion ofta för datorspel (särskilt från tiden före 3D-spelen). Exempel på sådana spel inkluderar Ultima VII, EarthBound, och Paperboy.
Källor och fotnoter
- Denna artikel är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Oblique projection, 25 augusti 2008.
- ↑ [http://mathworld.wolfram.com/PohlkesTheorem.html Weisstein, Eric W. "Pohlke's Theorem." From MathWorld--A Wolfram Web Resource. (engelska)]
- ↑ 2,0 2,1 Parallel Projections from PlaneView3D Online (engelska)
Mer läsning
Foley, James (1997). Computer Graphics. Boston: Addison-Wesley. ISBN 0201848406.