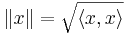Parallellogramlagen

Från Rilpedia

Version från den 15 februari 2009 kl. 19.23 av 79.136.62.147 (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Parallellogramlagen är inom matematik en ekvation som kan ses i olika sammanhang. Det enklaste sammanhanget är i vanlig geometri.

Geometri

I geometri säger parallellogramlagen att summan av kvadraterna av längderna av ett parallellograms sidor är lika med summan av kvadraterna av diagonalerna:

AB2 + BC2 + CD2 + AD2 = AC2 + BD2.

Normerade rum

I samband med normerade rum menas med parallellogramlagen följande ekvation:

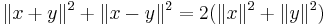\|x+y\|^2 + \|x-y\|^2 = 2(\|x\|^2 + \|y\|^2).

Alla normerade rum uppfyller inte denna ekvation. Om rummet är ett inre produktrum med en inducerad norm enligt:

\|x\| = \sqrt{\langle x, x \rangle}

så är parallellogramlagen sann. Omvänt, om en norm uppfyller parallellogramlagen kan man från normen göra en inre produkt via polarisationsidentiteten.

Hämtad från "https://sv.rilpedia.org/wiki/Parallellogramlagen"
Personliga verktyg