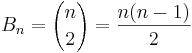Komplett graf
Från Rilpedia
Version från den 10 maj 2009 kl. 20.20 av Ptbotgourou (Diskussion)
En komplett graf är i det matematiska området grafteori en enkel graf där varje par av distinkta noder har en båge mellan sig. En komplett graf med n noder betecknas ofta Kn.
Egenskaper
Alla noder i en komplett graf har samma grad, n − 1.
Grafen Kn kan ses som en representation av en n − 1-simplex och är övre gräns för antal kopplingar i ett nätverk med n noder. Så att K3 representerar en triangel, K4 en tetraeder, osv.
Antalet bågar Bn i grafen Kn fås genom det enkla sambandet:
K1 till K4 är planära grafer, men K5 är inte planär, enligt Kuratowskis sats.
Exempel
Nedan finns en tabell med K1 till K8 och deras bågantal:
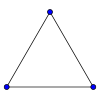
| K1:0 | K2:1 | K3:3 | K4:6 |
|---|---|---|---|
 |
 |
 |
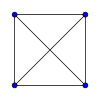 |
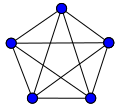
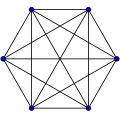
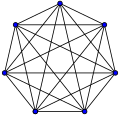
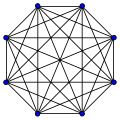
| K5:10 | K6:15 | K7:21 | K8:28 |
 |
 |
 |
 |