Arealteori för polygoner
Från Rilpedia
Liksidiga polygoner har många gånger fascinerat matematiker för deras regelbundna uppbyggnad. I en liksidig polygon skall alla sidor vara lika långa och vinkeldifferensen vara densamma i alla vinklar.
Vinkeldifferensen är densamma som det yttre gradtalet subtraherat med 360° kommer att bli den inre vinkeln av polygonen i °
På grund av sin regelbundet till storleken så är det inte alltför svårt att skapa formler för till exempel arean av olika liksidiga polygoner.
Nedan nämnda formel beskriver arean av en liksidig polygon.
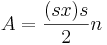
Teorin grundas på arean av en triangel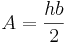 
Formel kan enkelt förklaras som en triangelindelning av den liksidiga polygonen där:
s= Sidan (basen av triangeln)
x=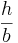 
vilket avslöjar förhållandet mellan basen och höjden i triangeln.
n= Antal hörn i den liksidiga polygonen (antal trianglar)
Det är alltså en förenkling för att beräkna arean av enskild till exempel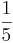 
i en pentagon, 
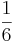i en hexagon etc, och sedan multiplicera denna area med n.
Produkten kommer då att bli arean av nämnda liksidiga polygon. Genom en ekvation mellan arean av valfri storlek av en liksidig polygon, kan du då ta reda på värdet av x, och sedan använda formeln för vilken annan storlek av den valda polygonen som helst.
