Uppräkneligt kompakt

Från Rilpedia

Version från den 24 februari 2008 kl. 20.46 av Yuide (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett topologiskt rum 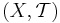(X,\mathcal{T}) är uppräkneligt kompakt om varje framställning av mängden X som en uppräknelig union av öppna mängder kan skrivas som en union av ett ändligt antal öppna mängder:

X = \bigcup_{n=1}^\infty O_n \quad \Longrightarrow \quad X = \bigcup_{k=1}^N O_{n_k}, \qquad O_n \in \mathcal{T}.

Denna definition är ekvivalent med följande egenskaper:

  • Varje oändlig delmängd av X har en omega-ackumuleringspunkt som är ett element i mängden X.
  • Varje följd av element i mängden X har en ackumuleringspunkt som är ett element i X.
  • Varje familj bestående av uppräkneligt många slutna delmängder vars snitt är icke-tomt, har en ändlig delfamilj av slutna mängder vars snitt också är icke-tomt.
Hämtad från "https://sv.rilpedia.org/wiki/Uppr%C3%A4kneligt_kompakt"
Personliga verktyg