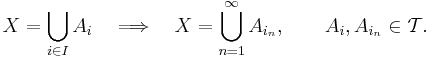Lindelöf-rum

Från Rilpedia

Version från den 10 april 2009 kl. 08.24 av Xqbot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett topologiskt rum 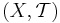(X,\mathcal{T}) säges vara ett Lindelöf-rum om varje framställning av mängden X som en union av öppna mängder, kan reduceras till en framställning av X som en union av uppräkneligt många öppna mängder:

X = \bigcup_{i\in I} A_i \quad \Longrightarrow \quad X = \bigcup_{n=1}^\infty A_{i_n}, \qquad A_i,A_{i_n} \in \mathcal{T}.

Se även


Nuvola apps kpovmodeler.svg Denna artikel om geometri är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Lindel%C3%B6f-rum"
Personliga verktyg