Superellips

Från Rilpedia

Texten från svenska Wikipedia

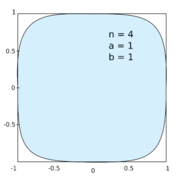
En kvirkel med n = 4.

En superellips, eller Lamékurva är en kurva som är relaterad till ellipsen.

Ekvationen för superellipser är:

,

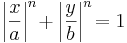där a är det största avståndet från ellipsens centrum till dess kontur, medan b är det kortaste, och n är en positiv exponent. När n = 2 beskriver ekvationen en ellips. Ekvationen med n större än 2 ger en mellanform av en ellips och en rektangel där rektangeln har utåtböjda sidor och rundade hörn.

Trafikplatsen vid Sergels torg i Stockholm har formen av en superellips med n = 5/2 och a/b = 6/5. Bruno Mathssons och Piet Heins superelliptiska bord har samma n och a/b = 3/2.

Referenser

• Sokolov, D. D., Lamé curve (2001) Springer Encyclopaedia of Mathematics.
• Weisstein, Eric W. (2006). ”Superellipse”. MathWorld. Wolfram. http://mathworld.wolfram.com/Superellipse.html. Läst 2007-07-22.