Nollvektor

Från Rilpedia

Texten från svenska Wikipedia

En nollvektor är i linjär algebra en vektor bestående endast av nollor, (0,0,...,0). En nollvektor brukar skrivas symboliskt som 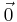, 0, eller helt enkelt 0.

Linjär algebra

I linjär algebra är nollvektorn definierad som det neutrala elementet för vektoraddition i ett vektorrum.

Egenskaper

• Nollvektorn är unik. Om a och b är nollvektorer gäller att a = a + b = b.
• Nollvektorn är resultatet vid skalärmultiplikation med skalären noll av alla vektorer.
• Mängden {0} är ett vektorrum med endast ett element.
• Nollvektorn är, av sig själv linjärt beroende, så att varje mängd av vektorer som innehåller nollvektorn är linjärt beroende.
• I ett normerat rum är nollvektorn den enda vektorn med norm lika med noll.

Seminormerade rum

I seminormerade rum kan det finnas flera vektorer vars seminorm är lika med noll. Dessa vektorer kallas ofta nollvektorer.