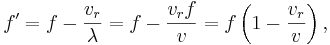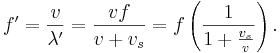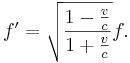Dopplereffekt

Från Rilpedia

Version från den 6 maj 2009 kl. 17.45 av Pieter Kuiper (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Illustration av Dopplereffekten och varför frekvensen mäts olika av en observatör när källan rör sig.

Dopplereffekt är ett fysikaliskt fenomen, som innebär en förändring av frekvensen (svängningstalet) hos en signal, till exempel ljud eller ljus, beroende på om källan närmar sig eller avlägsnar sig i förhållande till observatören. Först med att beskriva dopplereffekten var Christian Doppler 1842. Det allra lättast iakttagbara exemplet på dopplereffekten är sirenerna på ambulanser eller polisbilar, som tycks minska i frekvens då de passerar observatören. Bland annat en dopplerradar använder sig av dopplereffekten.

Ett annat exempel på dopplereffekten är de frekvensförändringar (dvs färgförändringar), orsakade av stjärnornas rörelse relativt jorden, som gör det möjligt för astronomer att mäta deras hastighet. Detta gör det bland annat möjligt att upptäcka planeter kring näraliggande stjärnor. Detta p.g.a. att hastigheten varierar beroende på om planeternas tyngdkraft drar stjärnan mot oss eller från oss. En liknande effekt är den s.k. rödförskjutningen hos avlägsna stjärnor eller galaxer, som orsakas av att de avlägsnar sig från oss med hög hastighet p.g.a. universums utvidgning. Skillnaden i det fallet är att källan inte rör sig i förhållande till rymden utan att det är rymden själv som utvidgar sig. Detta brukar inte kallas dopplereffekt.

Akustisk dopplereffekt

För vågor i ett medium som luft eller vatten är formlerna for dopplereffektens frekvensförändring olika för fallet där källan rör sig och fallet där mottagaren rör sig i förhållande till mediet.

När mottagaren rör sig med en hastighet 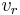v_r \, bort från sändaren, passerar mottagaren färre vågfronter. Frekvensen är därför lägre och blir:

f' = f - \frac{v_r}{\lambda} = f - \frac{v_r f}{v} = f \left(1 - \frac {v_r}{v} \right),

där f' är den frekvens som uppfattas av mottagaren, f frekvensen hos sändaren, λ våglångden och v hastigheten hos vågorna i mediet.

När källan rör sig bort från mottagaren med en hastighet 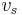v_s \,, blir avståndet mellan vågfronterna vid mottagaren större. Våglängden ser ut som 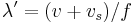\lambda' = (v+v_s)/f \,, så att

f' = \frac{v}{\lambda'} = \frac{vf}{v+v_s} = f \left(\frac{1}{1 + \frac {v_s}{v}} \right).

Vid hastigheter som är låga i förhållande till vågornas utbredningshastighet ger båda formler ungefär samma svar.

Elektromagnetisk dopplereffekt

För ljus och andra elektromagnetiska vågor spelar mediet ofta ingen roll. I vakuum beror frekvensförskjutningen endast på den relativa hastigheten mellan källa och mottagare. Den skiftade frekvensen är då given av:

f'=\sqrt{\frac{1-\frac{v}{c}}{1+\frac{v}{c}}}f.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Dopplereffekt"
Personliga verktyg