Fullständig (modellteori)
Från Rilpedia
Version från den 6 oktober 2006 kl. 19.32 av Spakoj (Diskussion)
Inom matematisk logik sägs en teori T vara fullständig om för varje sluten formel kan avgöras i T
Formell definition
Låt T vara en teori i ett språk S. T sägs vara fullständig om för varje sluten formel 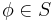 gäller antingen
gäller antingen
eller
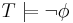
Detta villkor är ekvivalent med att T är maximal, dvs att det inte finns någon konsistent mängd formler T' så att
men
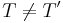
Exempel
- Givet en modell M så är mängden av formler sanna i M en fullständig teori
- Teorin för algebraiskt slutna kroppar är fullständig
- Teorin för en tät linjär ordning utan ändpunkter är fullständig
- Mer allmänt så är varje teori som är kategorisk i något kardinaltal fullständig.
- Teorin för differentiellt slutna kroppar är fullständig.
- Peanoaritmetiken är inte fullständig.
- Mer allmänt så är ingen rekursivt axiomatiserbar teori som interpreterar aritmetiken fullständig.



