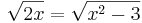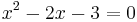Falska rötter
Från Rilpedia
Version från den 3 oktober 2008 kl. 14.13 av MenoBot (Diskussion)
Falska rötter kallas inom algebra lösningar till en ekvation N om
- Ursprungsproblemet var att finna lösningar till en ekvation M
- Ekvationen M genomgått en förändring, vanligen en kvadrering eller motsvarande, som resulterat i ekvationen N
- Lösningarna uppfyller ekvationen N, men inte M
Exempel
Finn x sådant att
Eftersom kvadratroten endast är definierad för argument större än eller lika med 0, så måste 2x och därmed även x vara positivt. Dessutom måste 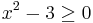 , vilket ger kravet
, vilket ger kravet 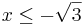 eller
eller 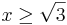 . Tillsammans ger dessa alltså att
. Tillsammans ger dessa alltså att 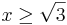 . Om vi kvadrerar uttrycket och flyttar runt får vi:
. Om vi kvadrerar uttrycket och flyttar runt får vi:
Detta uttryck har två lösningar, vilka man kan finna med kvadratkomplettering. De visar sig då vara x=-1 och x=3. Eftersom -1 är mindre än 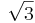 är det en falsk rot, medan x=3 är en korrekt lösning till det ursprungliga problemet.
är det en falsk rot, medan x=3 är en korrekt lösning till det ursprungliga problemet.