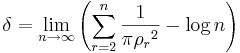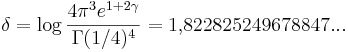Masser–Gramains konstant

Från Rilpedia

Version från den 1 januari 2009 kl. 18.19 av LA2-bot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Masser–Gramains konstant är en matematisk konstant definierad som

\delta = \lim_{n \to \infty} \left( \sum_{r=2}^n \frac{1}{\pi {\rho_r}^2} - \log n \right)

där ρr är radien på den minsta slutna cirkelskiva i det komplexa talplanet som innehåller minst r stycken gaussiska tal. Masser–Gramains konstant kan betraktas som en tvådimensionell generalisering av Eulers konstant γ.

F Gramain och M Weber har visat att

1,811447299 < δ < 1,897327117,

men konstantens exakta värde är okänt. Gramain lade fram den ännu obekräftade hypotesen

\delta = \log \frac{4 \pi^3 e^{1 + 2 \gamma}}{\Gamma(1/4)^4} = 1,\!822825249678847...

där Γ betecknar gammafunktionen.

Se även

Referenser

  • Julian Havil, Gamma: Exploring Euler's Constant, Princeton University Press 2003, s. 116-117.
  • Steven Finch, Masser-Gramain Constant
Hämtad från "https://sv.rilpedia.org/wiki/Masser%E2%80%93Gramains_konstant"
Personliga verktyg