Derivation
Från Rilpedia
Inom algebran, är en derivation en typ av avbildning som abstraherar deriveringsavbilningen i analysen.
Definition
Låt k vara en kommutativ ring och R en kommutativ k-algebra. En k-derivation på R är en k-linjär avbildning D från R till R som satisfierar Leibniz regel dvs:
- D(xy) = xDy + yDx
Exempel
- Låt R vara ringen av oändligt deriverbara funktioner och D avbildningen
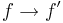
- Låt R vara ringen av polynom i variablen x över en kropp k, och låt D vara operatorn
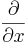
- Låt R vara ringen av polynom i variblerna x1,...,xn och låt D vara på formen
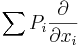
Egenskaper
Man kan visa att derivationerna på ringen av släta funktioner på en differentierbar mångfald svarar entydigt mot vektorfälten på mångfalden. Detta ger en remarkabel koppling mellan analytiska och rent algebraiska objekt.
Inom algebra och algebraisk geometri används derivationer för att ge motsvarigheter till den analytiska teori som finns för differentierbara mångfalder. Derivationer kan också användas i rent algebraiska syften, till exempel för att klassificera extensioner av kommutativa algebror, eller för att karakterisera helt slutna ringar.



