Diffeomorfi

Från Rilpedia

Version från den 7 april 2009 kl. 00.27 av Calle (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
En diffeomorfi av en kvadrat.

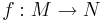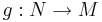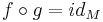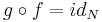I differentialgeometri är en diffeomorfi en form av isomorfi mellan differentierbara mångfalder. En funktion f:M\rightarrow N är en diffeomorfi om den är slät, dvs oändligt differentierbar, och det finns en funktion g:N\rightarrow M som också är slät så att f\circ g=id_M och g\circ f=id_N.

Exempel

  • För varje differentierbar mångfald M så är identitetsfunktionen en diffeomorfi från M till M.
  • Funktionen 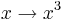x\rightarrow x^3 på R har en invers x\rightarrow x^{\frac{1}{3}}, men är inte en diffeomorfi eftersom inversen inte är slät.
  • Funktionen x\rightarrow \frac{1}{x} är en diffeomorfi mellan (0,1) och R +

Diffeomorfier i {\mathbb{R}}^n

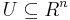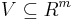Givet öppna mängder U\subseteq R^n och V\subseteq R^m och en funktion 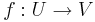f:U\rightarrow V så är f en diffeomorfi omm:

  1. f är bijektiv
  2. Jacobianen för f är nollskild i varje punkt.

Villkor 2 medför att det inte finns några diffeomorfier mellan U och V om n är skilt från m.

Hämtad från "https://sv.rilpedia.org/wiki/Diffeomorfi"
Personliga verktyg