Existentiellt sluten

Från Rilpedia

Version från den 6 januari 2006 kl. 20.49 av Spakoj (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

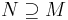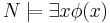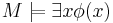Inom modellteorin sägs en modell M för en teori T vara existentiellt sluten om för varje formel φ(x) med parametrar i M sådan att det finns N så att N\supseteq M och N\models\exists x\phi(x) så gäller M\models\exists x\phi(x).

Exempel

  1. Algebraiskt slutna kroppar är existentiellt slutna, enligt Chevalleys sats och Hilberts nollställesats.
  2. Z, ringen av heltal, är existentiellt sluten

En teori vars modeller alltid är existentiellt slutna sägs vara modellfullständig.

Hämtad från "https://sv.rilpedia.org/wiki/Existentiellt_sluten"
Personliga verktyg