Monty Hall-problemet

Från Rilpedia

Texten från svenska Wikipedia

På jakt efter en ny bil väljer den tävlande dörr 1. Monty väljer nu att visa att bakom dörr 3 finns en get. Ska den tävlande byta dörr eller inte?

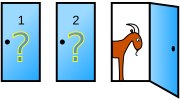
Monty Hall-problemet är ett spelteoretiskt problem som bygger på sannolikheter. Det är löst baserat på det amerikanska spelet "Let's make a deal". Namnet kommer från spelets presentatör, Monty Hall. I spelet får spelaren se tre dörrar - bakom en finns en bil, och bakom de två andra finns två getter. Spelet börjar med att spelaren får välja en dörr, utan att öppna den. Därefter öppnar presentatören, som vet vad som finns bakom dörrarna, en av de två resterande dörrarna och visar att denna dörr inte innehåller vinsten. Spelaren får då ytterligare ett val, nämligen att byta dörr.

Frågeställningen är om chanserna att vinna ökar om spelaren byter dörr.

Problemet kallas ibland Monty Hall-paradoxen då den korrekta lösningen motsäger ett intuitivt resonemang om sannolikheterna för att göra rätt val.

Problem och lösning

Problemet

Craig F. Whitaker formulerade problemet i en insändare till Marilyn vos Savants kolumn i Parade Magazine 1990. Denna formulering blev berömd då hennes svar orsakade kontrovers.

Antag att du är med i en tv-lek där du får välja mellan tre dörrar. Bakom en dörr finns en bil, bakom de andra två, getter. Du väljer dörr 1, och tv-värden, som vet vad som finns bakom alla dörrar, öppnar en annan dörr, säg nummer 3, vilken visar en get. Han frågar därefter: "Vill du byta till dörr nummer 2?". Är det då till din fördel att ändra ditt val?

Lösningen

Ja, det är till din fördel att ändra ditt val. Chansen att vinna dubbleras av att ändra sitt val jämfört med att hålla fast vid originalvalet.

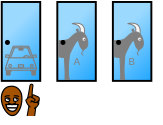
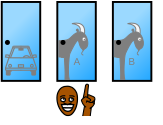
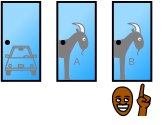
Lösningen kan visualiseras genom att visa att det finns tre olika scenarion, samtliga med 1/3 sannolikhet:

• Spelaren väljer förlust 1. Spelledaren väljer förlust 2. Byte ger vinst
• Spelaren väljer förlust 2. Spelledaren väljer förlust 1. Byte ger vinst
• Spelaren väljer vinst. Spelledaren väljer förlust 1 eller 2. Byte ger förlust

Som synes är det bara om man valde rätt dörr till att börja med som det kan bli fel om man byter. Då det är 1/3 chans att man valde rätt dörr från början blir det också bara 1/3 chans att man förlorar om man byter, och således 2/3 chans att bytet ger vinst.

Förståelse av lösningen

1. Presentatören visar en av getterna Spelaren väljer bilen (sannolikhet 1/3) Byte resulterar i en av getterna 2. Presentatören måste visa get B Spelaren valde get A (sannolikhet 1/3) Byte ger vinst 3. Presentatören måste visa get A Spelaren valde get B (sannolikhet 1/3) Byte ger vinst

Spelaren har lika stor chans att initialt välja bilen, get A eller get B. Byte ger vinst i 2/3 av fallen.

Varianter

Obestämt antal dörrar

En generalisering av problemet är att använda n antal dörrar. I det första steget väljer du då en dörr, varefter spelledaren öppnar en dörr med en get bakom. Du får sedan valet att stå fast vid ditt val eller byta. Detta fortsätter tills det bara är två oöppnade dörrar kvar. Frågeställningen är huruvida, och i så fall, hur många gånger, du bör byta dörr, och när?

Den bästa strategin är att hålla fast vid sitt val ända tills på slutet, då du byter. Med denna stategi är sannolikheten att vinna (n-1)/n, vilket bevisades av Bapeswara Rao och Rao.