Ordo
Från Rilpedia
Ordo (latin för ordning) är ett begrepp inom matematik och datavetenskap och används för att mäta hur tung en term är. Till exempel betyder O(n2) eller O(n3) att den största betydande termen är n2 eller n3. Inom datavetenskap, särskilt komplexitetsteori, används det för att beskriva algoritmers effektivitet.
Inom matematik används ordo för olika typer av uppskattningar. En funktion f(x) sägs vara "stort ordo" g(x) då x 0 om f(x)/g(x) är begränsad då x
0 om f(x)/g(x) är begränsad då x 0. Detta skrivs
0. Detta skrivs
- f(x) = O(g(x)) då x
 0.
0.
Ofta utelämnar man "x 0" om det framgår av sammanhanget att det gäller i närheten av origo och skriver bara f(x) = O(g(x)).
0" om det framgår av sammanhanget att det gäller i närheten av origo och skriver bara f(x) = O(g(x)).
f(x) sägs vara "litet ordo" g(x) då x 0 om f(x)/g(x)
0 om f(x)/g(x) 0 då x
0 då x 0, vilket skrivs
0, vilket skrivs
- f(x) = o(g(x)) då x
 0.
0.
Ordobegreppet används i praktiska sammanhang vid Taylor- och Maclaurinutvecklingar som beteckning på resttermerna (Forsling och Neymark 2004. Matematisk analys, en variabel).
Exempel: sin(x) =1-x3/6+O(x5) då x 0.
0.
Relaterade notationer
| Den här artikeln anses undermålig och kan behöva skrivas om helt för att leva upp till Wikipedias artikelstandard. Diskutera frågan på diskussionssidan och förbättra gärna artikeln. Var uppmärksam på artikelns innehåll. Motivering: Jfr beskrivning en:Big O notation |
| Notation | I ord | Definition |
|---|---|---|
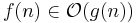 |
f växer högst lika snabbt som g | 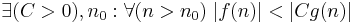 |
 |
f växer minst lika snabbt som g | 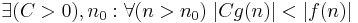 |
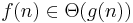 |
f växer lika snabbt som g | 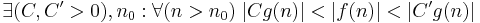 |
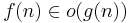 |
f växer långsammare än g | 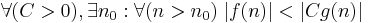 |
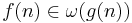 |
f växer snabbare än g | 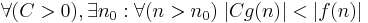 |
| f(n) ˜ g(n) | asymptotiskt lika | 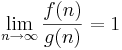 |
Se även
- Ordo (tidning), var en vetenskaplig tidskift utgiven av Lunds Universitet.



