Rekursiv funktion
Från Rilpedia
Rekursiv funktion, en matematisk funktion som definieras med hjälp av rekursion, d.v.s. med hjälp av referenser till sig själv. För att en definition av en rekursiv funktion skall vara korrekt måste den innehålla minst ett basfall som inte refererar till funktionen själv, mer komplicerade fall kan sedan referera till basfallen.
Ett exempel är definitionen av fakultet, som kan skrivas rekursivt. Fakulteten av talet n (n!) är produkten av talen 1, 2, 3 ... n.
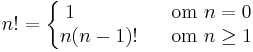
Denna definition leder för fallet 3! till följande steg:
3! = 3 · (3-1)!
= 3 · 2!
= 3 · 2 · (2-1)!
= 3 · 2 · 1!
= 3 · 2 · 1 · (1-1)!
= 3 · 2 · 1 · 0!
= 3 · 2 · 1 · 1
= 6
Exempel
Ett känt exempel är definitionen av Fibonaccitalen.
Man kan använda rekursion för att härleda det minsta antal flyttningar som krävs för att lösa problemet Tornen i Hanoi. Om man låter an beteckna det minsta antalet flyttningar som krävs för att flytta ett hanoitorn med n skivor så erhålls rekursionen an=2an-1+1; a1=1. Denna (rekursiva) differensekvation har ingen uppenbar lösning, men genom att räkna ut ett fåtal termer i början kan man göra en gissning som därefter kan bevisas medelst induktion över n. Denna gissning är lämpligen 2n-1, som är konsistent med rekursionen och startvillkoret.
Rekursiva funktioner är ett centralt begrepp inom den diskreta matematiken och datavetenskapen. Det har till exempel visats att rekursiva funktioner är precis de funktioner som kan beräknas av turingmaskiner.
Inom funktionell programmering använder man rekursiva funktioner istället för loopar. Eftersom varje delsteg måste sparas vid beräkningen av en rekursiv funktion sker det ibland en optimering vid kompilering eller interpretering av dessa språk som ersätter rekursiva beräkningar med loopar.



