Spektrum (funktionalanalys)

Från Rilpedia

Version från den 2 maj 2009 kl. 10.35 av VolkovBot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom funktionalanalysen så är spektrumet för en operator en generalisering av egenvärdesbegreppet, som är mycket mer användbar i fallet med oändligt-dimensionella rum. Till exempel så saknar heltalsskift-operatorn på Hilbertrummet 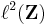\ell^2(\mathbf Z) egenvärden, men det gäller allmänt att en begränsad linjär operator på ett komplext Banachrum har icke-tomt spektrum.

Definition

Låt X vara ett komplext Banachrum. Då är spektrumet för en begränsad linjär operator T : X → X en delmängd av de komplexa talen betecknad σ(T). Per definition gäller att λ ∉ σ(T) om och endast om λI − T är inverterbar samt (λI − T) − 1 är en begränad operator på X.

Här betecknar I identitetsoperatorn på X.


Lebesgue Icon.svg Denna artikel om matematisk analys är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Spektrum_(funktionalanalys)"
Personliga verktyg