Bernsteinpolynom

Från Rilpedia

Version från den 26 oktober 2008 kl. 14.59 av TXiKiBoT (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett Bernsteinpolynom är ett polynom och definieras som

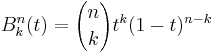
B^n_k(t) = {n \choose k} t^k (1-t)^{n-k}

Parametern t hålls inom intervallet [0,1] och polynomet kommer att ha ett maximum då 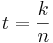t=\frac{k}{n}. Nedan är 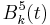B^5_k(t) utritad för olika värden på k.

Bernsteinpolynom.png


En viktig egenskap hos Bernsteinpolynomen är att

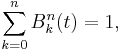
\sum^n_{k=0} B^n_k(t) = 1,

för alla t, vilket gör att man kan addera punkter med hjälp av Bernsteinpolynom.

Derivata

Bernsteinpolynomen har följande derivata:

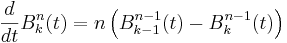\frac{d}{dt}B^n_k(t) = n \left( B^{n-1}_{k-1}(t) - B^{n-1}_{k}(t) \right).

Hämtad från "https://sv.rilpedia.org/wiki/Bernsteinpolynom"
Personliga verktyg