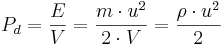Tryck

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
För tryck som grafisk teknik (tryck av böcker etc), se tryckteknik.
För tryck som fonetisk term (tryckaccent), se fonetik.

Tryck är inom fysiken det samma som kraft per ytenhet. Tryckenheten i SI-systemet är 1 pascal (1 Pa = 1 newton per kvadratmeter, N/m²). Då pascal är en liten enhet, brukar ofta andra tryckenheter användas, till exempel: Bar, Psi, mmHg, mVp, mmVp samt atm.

Omvandlingstabell för tryckenheter
Enhet Motsvarighet i kPa Motsvarighet i bar Motsvarighet i PSI Motsvarighet i mmHg Motsvarighet i mmVp Motsvarighet i mVp Motsvarighet i atm
bar 100 1 14,5 750,06 10190 10,19 0,99
PSI 6,89 0,069 1 51,71 703 0,70 0,068
mmHg 0,13 0,0013 0,019 1 13,59 0,01359 0,0013
mmVp 0,0098 98·10-6 0,0014 0,074 1 0,001 97·10-6
mVp 9,81 0,098 1,42 73,56 1000 1 0,097
atm 101,325 1,01325 14,70 760 10 330 10,33 1

Instrument för mätning av tryck är barometer och manometer.


Undervattensfarkoster måste stå emot starkt tryck utifrån.
På hög höjd är lufttrycket lägre än vid havsytan. Därför är det svårt att andas om man inte är i en lufttät flygkabin.


Innehåll

Lufttryck

Huvudartikel: Lufttryck

Lufttrycket är det tryck som atmosfären åstadkommer. Ju högre ovanför havets yta som man befinner sig, desto mindre blir lufttrycket, eftersom man då har en mindre del utav atmosfären ovanför sig. Man har försökt bestämma ett medelvärde för lufttrycket i olika standarder. STP och NTP är exempel på sådana standarder. I dessa två standarder anges det normala lufttrycket vid havsytan som 1 atm, d.v.s. 101,325 kPa.

Hydrostatiskt tryck

Med det hydrostatiska trycket avses det tryck som en vätska (vanligtvis vatten) åstadkommer. Under vattenytan ökar trycket med ca 1 bar för var tionde meter. Det totala trycket som råder på en bestämd punkt på jorden är summan av lufttrycket och det eventuella hydrostatiska trycket.

Härledning av formeln för det hydrostatiska trycket

Låt oss tänka oss en vattenpelare, som har sin topp vid vattenytan, och som sträcker sig ända ner till en bestämd nivå. Avståndet ifrån denna nivå upp till ytan är h, som samtidigt är vattenpelarens höjd. Denna vattenpelare åstadkommer ett tryck på sin bottenarea A enligt

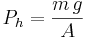
P_h = \frac{m\,g}{A}

där Ph är hydrostatiskt tryck, m massan, g tyngdaccelerationen och A arean. En kropps massa kan skrivas som 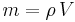m = \rho\,V

där ρ är densiteten och V är volymen. Detta ger:

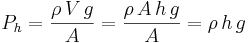
P_h = \frac{\rho\,V\,g}{A} = \frac{\rho\,A\,h\,g}{A} = \rho\,h\,g

Det totala trycket vid en bestämd punkt räknas då enligt:

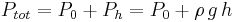
P_{tot} = P_0 + P_h = P_0 + \rho\,g\,h

där P0 är lufttrycket.

Hydrodynamiskt tryck

Med det hydrodynamiska trycket avses den rörelseenergi, som vatten och andra inkompressibla fluider åstadkommer vid rörströmning och kanalströmning. Om vattnets rörelseenergi delas med dess volym, blir SI-enheten Pascal. Om man tänker sig att en ideal inkompressibel fluid passerar genom en plan sektionsförändring, så blir summan av det hydrostatiska och hydrodynamiska trycket konstant, det vill säga:

P_{h,1} + P_{d,1} = P_{h,2} + P_{d,2} \Rightarrow P_{h,1} - P_{h,2} = P_{d,2} - P_{d,1}

där Ph är hydrostatiskt och Pd är hydrodynamiskt tryck.

I verkligheten sker alltid en tilläggsförlust (ht) vid alla sektionsförändringar, varför uttrycket får skrivas

Ph,1 + Pd,1 = Ph,2 + Pd,2 + ht

Härledning av formeln för det hydrodynamiska trycket

Den klassiska formen för rörelseenergin E brukar skrivas

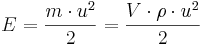
E = \dfrac {m \cdot u^2}{2} = \dfrac {V \cdot \rho \cdot u^2} {2}

Genom att dela vattenkroppens totala rörelseenergi (E) med dess volym (V), erhålls det hydrodynamiska trycket (Pd) enligt följande:

P_d = \dfrac {E}{V} = \dfrac {m \cdot u^2}{2 \cdot V} = \dfrac {\rho \cdot u^2}{2}

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Tryck"
Personliga verktyg