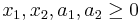Simplexmetoden

Från Rilpedia

Texten från svenska Wikipedia

Simplexmetoden eller simplexalgoritmen är en metod inom optimeringsläran för att effektivt lösa linjärprogrammeringsproblem. Metoden uppfanns av den amerikanske matematikern George Dantzig och är i dag den i särklass mest använda algoritmen för att lösa LP-problem som nästan helt dominerar den kommersiella marknaden.

Enligt linjärprogrammeringens fundamentalsats erhålles alltid optimum i minst en hörnpunkt till den tillåtna mängden och dessa hörn motsvaras av en (eller flera i det degenererade fallet) baslösning(ar). Simplexmetoden söker den bästa lösningen genom att systematisk flytta sig från en baslösning till en annan närliggande på ett sådant sätt att målfunktionsvärdet förbättras. Den söker inte igenom samtliga hörnpunkter då det även för förhållandevis "små" LP-problem finns oerhört många men eftersom problemet är konvext kommer den hörnpunkt för vilka ingen närliggande hörnpunkt har ett bättre målfunktionsvärde att vara optimallösningen till problemet.

Basbyten

Givet en tillåten baslösning $x 0$ till ett LP-problem kan en söriktning $d 0$ bestämmas för varje icke-basvariabler. Riktningen svarar mot att variabeln i fråga tillåts växa och övriga variblers värden erhålls ur bivillkoren den tidigare icke-basvariabel som tillåts bli nollskild kallas för ingående basvariabel.

Om det tillåtna området är begränsad finns det en största steglängd $t 0$ för vilken den nya punkten $x 1 = x 0 + t 0 * d 0$ är en tillåten punkt (dvs alla variabler 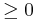$\ge 0$ ) den variabel som först når noll begränsar steglängden och kallas utgående basvariabel. Om $d i$ och $t i$ väljs på detta sätt i varje iteration kommer den nya lösningen $x i + 1$ att vara en tillåten baslösning Att på detta sätt röra sig mellan olika lösningar kallas för basbyte.

Simplexmetoden iterar på samma sätt mellan tillåtna baslösningar med det tillägget att sökriktningen endast får väljas så att målfunktionen förbättras. (inte sällan finns flera alternativ det har då visat sig bra att välja den riktning som snabbast förbättrar målfunktionen man säger att den har bäst reducerande kostnad, det är emmellertid inte garanterat att det ger den enklaste lösningen).

Eftersom målfunktion ständigt förbättras och antalet baslösningar är ändligt (om än stort) är simplexmetoden garanterad att finna lösningen.

För att lösa ett generellt LP-problem måste det först överföras till standardform därefter måste en tillåten baslösning identfieras.

Algoritmen

(Försteg) Börja med en tillåten baslösning $x 0$ sätt iterationsräknaren k till 0.
(Steg 1) Beräkna reducerande kostnader för alla icke-basvariabler eventuellt genom omskrivning av målfunktion.
Sätt den variabel med bäst reducerande kostnadad till inkommande variabel. Om ingen förbättrande finns är lösningen funnen.
Beräkna sökriktning $d k$ och bestäm steglängden $t k$ till det största tal för vilket $x k + d k t k$ är en tillåten lösning. (om t tillåts gå mot oändligheten har problemet obegränsad bra lösning).
Sätt $x k + 1 = x k + d k t k$ stega vidare k := k+1 och gå till steg 1.

Illustrerande exempel

Betrakta LP-problemet

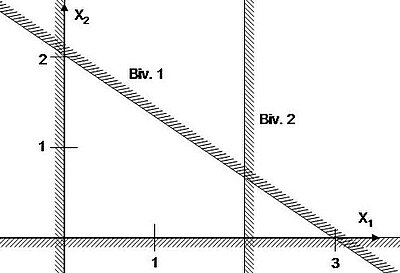
Ett mycket litet exempel på ett LP-problem

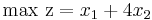
$\mbox{max z} = x_1 + 4x_2 \,$

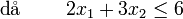$\mbox{då} \qquad\ 2x_1 + 3x_2 \le 6$ Bivillkor 1

$x_1 \le 2$ Bivillkor 2

$x_1,x_2 \ge 0$

Som kan överföras på standarform genom introduktion av slackvariablerna $a 1$ och $a 2$ enligt:

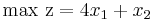
$\mbox{max z} = 4x_1 + x_2 \,$

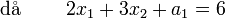
$\mbox{då} \qquad\ 2x_1 + 3x_2 + a_1 = 6$

$x_1 + a_2 = 2 \,$

$x_1,x_2,a_1,a_2 \ge 0$

Vi kan enkelt identifiera ur figuren att $x 1 = x 2 = 0$ är en tillåten lösning som ger upphov till ekvationssystemet

$0 + 0 +a_1 = 6 \,$

$0 + a_2 = 2 \,$

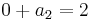
vilket ger upphov till baslösningen där $a 1, a 2$ är basvariabler lika med 6 respektive 2 och $x 1, x 2$ är icke basvariabler ( = 0).

Ur målfunktion kan vi utläsa att en ökning av $x 1$ innebär en ökning av z med 4 enheter/enhet samt att motsvarande värde för $x 2$ är ett (de reducerande kostnaderna är 4 respektive 1). Eftersom båda icke-basvariabler ger förbättrande sökrikningar tar vi den snabbaste och väljer $x 1$ som inkommande basvariabel.

Ur omskrivningen av bivillkoren erhålles

$a 1 = 6 - 2 x 1 - 3 x 2$

$a 2 = 2 - x 1$

Vilket motsvarar en sökriktning längs $x 2$ , $d 0$ = [0 1 -2 -1]

och vi ser att $a 2$ först kommer nå noll när $x 1$ ökar (detta sker för $x 1 = 2$ så $t 0 = 2$ ) dvs $a 2$ blir utgående basvariabel och vår nya baslösning blir att $a 1, x 1$ är basvariabler lika med 4 respektive 2 och $a 2, x 2$ är ickebasvariabler ( = 0).

Inför nästa iteration måste målfunktionen uttryckas i icke-basvariabler (så att vi kan se hur de påverkar) detta görs med hjälp av ekvationerna i bivillkoren.

$z = 8 - 4 a 2 + x 2$

Här erhålles att $x 2$ genererar en förbättrande riktning medans $a 2$ inte gör det. Vi kan också se att optimallösningen kommer vara minst 8 eftersom det är en konstantterm i målfunktion i sig inte ett viktigt resultat men bra för kontroll senare.

proceduren upprepas och vi når i $x 1 = 2 x 2 = 2 / 3, a 1 = a 2 = 0$ omskrivningen av målfunktion ger

$z = 10 - 4 a 2 - a 1 / 3$

Här kan ingen förbättrande sökriktning hittas (om $a 1$ eller $a 2$ ökar minskar z) vilket innebär att baslösningen är optimalösningen och funktionsvärdet är 10.

Källor

Lundgren, Jan & Rönnqvist, Mikael & Värbrand Peter: Optimeringslära, 2003, upplaga 3:1. ISBN 978-91-44-05314-1.

Simplexmetoden

Från Rilpedia

Innehåll

Basbyten

Algoritmen

Illustrerande exempel

Källor

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk