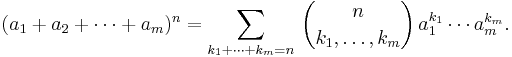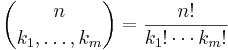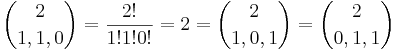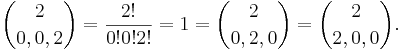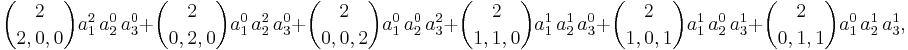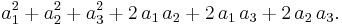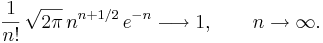Multinomialsatsen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Multinomialsatsen är, inom matematik, en generalisering av binomialsatsen och är en framställning av ett multinom (a_1+\cdots+a_m)^n som en summa av potenser i talen a_1,\dots,a_m.

Satsens lydelse

Låt 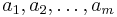a_1,a_2,\dots,a_m vara godtyckliga reella eller komplexa tal och n ett godtyckligt naturligt tal. Då kan potensen 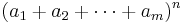(a_1+a_2+\cdots+a_m)^n framställas som följande summa:

(a_1+a_2+\cdots+a_m)^n = \sum_{k_1+\cdots+k_m=n} \, \binom{n}{k_1,\dots,k_m} \, a_1^{k_1}\cdots a_m^{k_m}.

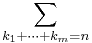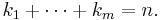Summasymbolen \sum_{k_1+\cdots+k_m=n} indikerar att man skall summera över alla multipler (k_1,\dots,k_m) av naturliga tal sådana att deras summa k_1 + \cdots + k_m = n. Symbolen

\binom{n}{k_1,\dots,k_m} = \frac{n!}{k_1!\cdots k_m!}

kallas multinomialkoefficient och är en generalisering av binomialkoefficienten 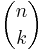\binom{n}{k}.

Exempel: Trinom

Trinomet (a1 + a2 + a3)2 kan beräknas direkt genom utveckling av kvadraten eller genom att använda multinomialsatsen.

Multinomialsatsen kräver att vi studerar tripler (k1,k2,k3) där komponenterna k1,k2 och k3 är heltal i mängden {0,1,2} sådana att deras summa är k1 + k2 + k3 = 2. De möjliga triplerna är 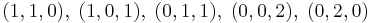(1,1,0),\;(1,0,1),\;(0,1,1),\;(0,0,2),\;(0,2,0) och (2,0,0).

Vi kan notera att problemet att bestämma de möjliga triplerna är identiskt med problemet att finna antalet sätt som man kan skriva talet 2 som en summa av tre naturliga tal. Den generella multinomialsatsen kräver att vi studerar problemet att bestämma antalet sätt som man kan skriva det naturliga talet n som en summa av m stycken naturliga tal.

Multinomialkoefficienterna associerade med de olika triplerna ovan är:

\binom{2}{1,1,0} = \frac{2!}{1!1!0!} = 2 = \binom{2}{1,0,1} = \binom{2}{0,1,1}

och

\binom{2}{0,0,2} = \frac{2!}{0!0!2!} = 1 = \binom{2}{0,2,0} = \binom{2}{2,0,0}.

Multinomialsatsen ger oss potensen (a1 + a2 + a3)2 som summan:

\binom{2}{2,0,0}a_1^2 \, a_2^0 \, a_3^0 + \binom{2}{0,2,0}a_1^0 \, a_2^2 \, a_3^0 + \binom{2}{0,0,2}a_1^0 \, a_2^0 \, a_3^2 + \binom{2}{1,1,0}a_1^1 \, a_2^1 \, a_3^0 + \binom{2}{1,0,1}a_1^1 \, a_2^0 \, a_3^1 + \binom{2}{0,1,1}a_1^0 \, a_2^1 \, a_3^1,

vilket, med de beräknade multinomialkoefficienterna, är

a_1^2 + a_2^2 + a_3^2 + 2 \, a_1 \, a_2 + 2 \, a_1 \, a_3 + 2 \, a_2 \, a_3.

Storleken hos n!: Stirlings formel

Symbolen n! kan uppfattas som antalet sätt att ordna n stycken objekt i en rad. Detta antal blir snabbt mycket stort:

Man kan ordna tio objekt i en rad på 3 628 800 olika sätt och 20 objekt i en rad på 2 432 902 008 176 640 000 olika sätt.

Det finns ett resultat som kallas Stirlings formel som ger information om hur snabbt talet n! växer med heltalet n:

\frac{1}{n!} \, \sqrt{2\pi} \, n^{n+1/2} \, e^{-n} \longrightarrow 1, \qquad n \to \infty.

För stora värden på n (Hur stora? är en intressant fråga) är n! ungefär lika stort som talet nn. Vi ser att n = 10 inte är tillräckligt stort, eftersom talet 10! är av storleksordningen 107, men att redan n = 20 närmar sig eftersom talet 20! är av storleksordningen 1019.

Hämtad från "https://sv.rilpedia.org/wiki/Multinomialsatsen"
Personliga verktyg