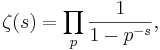Millennieproblemen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Millennieproblemen är sju berömda problem inom matematiken som ännu är olösta. Clay Mathematics Institute instiftade 2000 ett pris på 1 miljon dollar för lösningen av varje enskilt problem.

Innehåll

Problemen

De sju millennieproblemen är:

P=NP?

Det här är ett problem inom teoretisk datalogi och handlar om huruvida två klasser av beräkningsproblem, P och NP, är olika eller inte.

Problemet lyder:

  • Finns det något beräkningsproblem som kan lösas av en icke-deterministisk turingmaskin i polynomiell tid, det vill säga det ligger i komplexitetsklassen NP, men inte av en deterministisk turingmaskin, det vill säga det ligger inte i komplexitetsklassen P?

Det anses allmänt att svaret är ja. En stor klass beräkningsproblem har visats vara NP-fullständiga. Ett problem är NP-fullständigt om det har egenskapen att om det finns en polynomiell deterministisk algoritm för problemet, så finns en polynomiell deterministisk algoritm för alla problem i NP.

Ett bevis för existensen av ett beräkningproblem som ligger i NP men inte i P skulle alltså innebära att inget NP-fullständigt problem ligger i P.

Hodgeförmodan

Hodgeförmodan är ett problem i algebraisk geometri. Låt X vara en projektiv, icke-singuljär algebraisk varietet över de komplexa talen. Då finns de Rham-kohomologigrupper Hn(X,C) som har en hodgedekomposition 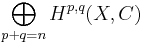\bigoplus_{p+q=n} H^{p,q}(X,C) Hodgeförmodan handlar om de rationella klasserna i diagonalen i denna dekomposition, alltså gruppen 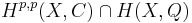H^{p,p}(X,C)\cap H(X,Q) av hodgeklasser. Nämligen, varje algebraisk cykel Z av kodimension p i X ger upphov till en kohomologiklass i H2p(X,Z) vars bild i H2p(X,Z) man kan visa är av typ (p,p). Därför finns en homomorfi från gruppen av cykler av kodimension p till gruppen av (p,p)-hodgeklasser. Hodgeförmodan säger nu att varje hodgeklass är en rationell linjärkombination av algebraiska cykler.

Poincarés förmodan

Poincarés förmodan är ett problem inom algebraisk topologi som handlar om huruvida 3-sfären karakteriseras av sin fundamentalgrupp. Närmare bestämt, till varje sammanhängande topologisk mångfald kan man associera en grupp, fundamentalgruppen som består av ekvivalensklasser av slutna loopar med en viss baspunkt, där två loopar är ekvivalenta om de kontinuerligt kan deformeras till varandra, och produkten av två loopar utgörs av deras union.

Man kan nu visa att en n-sfär, alltså mängden av punkter i Rn + 1 med avstånd 1 från origo, har en trivial fundamentalgrupp, dvs alla loopar är ekvivalenta. En topologisk mångfald med denna egenskap kallas enkelt sammanhängande. Man kan relativt enkelt visa att en omvändning till detta påstående är sann för n=2, nämligen; Varje kompakt enkelt sammanhängande mångfald av dimension 2 är homeomorf med 2-sfären.

Poincarés förmodan utgörs av motsvarande påstående i tre dimensioner:

Varje kompakt, enkelt sammanhängande 3-dimensionell mångfald är homeomorf med 3-sfären.

Under 1900-talets andra del visades att motsvarigheten till Poincares förmodan i dimensioner högre än 3 är sann. Dessa resultat är mycket djupa och har belönats med 2 fieldsmedaljer.

Nyligen har ett bevis för Poincarés förmodan presenterats av Grigorij Perelman. Närmare bestämt påstår sig Perelman visa Thurstons geometriseringsförmodan som medför Poincarés förmodan. Beviset är för närvarande under granskning, men har redan förklarats korrekt av flera experter.

Riemannhypotesen

Huvudartikel: Riemannhypotesen

Riemannhypotesen rör Riemanns zeta-funktion, ζ, som definieras som 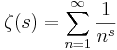\zeta (s)=\sum_{n=1}^\infty \frac{1}{n^s} för komplexa tal med 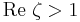\mathrm{Re} \ \zeta >1, och sedan kan fortsättas analytiskt till komplexa planet med en pol i 1. Funktionen har triviala nollställen i alla negativa jämna heltal. Riemannhypotesen säger att alla icke-triviala nollställen till zetafunktionen har realdel lika med 1/2.

På grund av produktrepresentationen

\zeta(s) = \prod_{p} \frac{1}{1-p^{-s}},

där produkten tas över alla primtal, är hypotesen intressant vid studiet av primtalens fördelning. Ett bevis för Riemannhypotesen skulle till exempel ge information om resttermen i primtalssatsen.

Man har hittills hittat över en miljard nollställen som uppfyller Riemannhypotesen, men ett bevis saknas fortfarande.

Yang-Mills-teori

Huvudartikel: Gaugeteori

Navier-Stokes ekvationer

Birch-Swinnerton-Dyers förmodan

Birch-Swinnerton-Dyers förmodan tillhör området aritmetisk algebraisk geometri. Låt E vara en elliptisk kurva, det vill säga en icke-singulär, projektiv kurva av genus 1, definierad över en talkropp K. Man kan visa att de K-rationella punkterna bildar en grupp under den additionsoperation som ges av att tre kolinjära punkter summerar till 0. Denna grupp består av en torsionskomponent samt ett antal kopior av Z. Detta antal kallas rangen för E.

Associerad till E finns också en meromorf funktion L(E,s), kallas L-funktionen för E. Den definieras som en viss eulerprodukt där faktorerna beror på antalet punkter på E över de ändliga kropparna.

Birch-Swinnerton-Dyers förmodan lyder:

  • Rangen för E är lika med nollställeordningen för L i 1.

Till exempel innebär alltså förmodan att gruppen av rationell punkter är en ändlig grupp om L-funktionen inte har ett nollställe i 1.

Externa länkar

E-to-the-i-pi.svg Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Millennieproblemen"
Personliga verktyg