Lagrangemultiplikator
Från Rilpedia
|
Lagrangemultiplikatorer är en metod i matematisk analys som kan användas om man vill hitta alla extrempunkter på funktionen f(x,y) när den begränsas av ett bivillkor g(x,y)=0. Metoden är namngiven efter Joseph Louis Lagrange och baseras på följande teorem.
Antag att två funktioner f(x,y) samt g(x,y) har kontinuerliga förstaderivator i punkten P0=(x0,y0) på kurvan C med ekvationen g(x,y)=0. Antag också att när f(x,y) begränsas av punkter på C så har funktionen alltid ett lokalt maximum eller minimum i P0.
Antag även att:
1. P0 är inte en slutpunkt på C 2.g(x,y)
0
Då finns ett tal, λ0, sådant att (x0,y0) är en stationär punkt för Lagrangefunktionen
L(x,y,λ) = f(x,y) + λg(x,y)
där λ är en Lagrangemultiplikator.
Bevis
1 och 2 tillsammans antyder att C är tillräckligt jämn för att ha en tangent igenom P0 och att 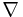g(P0) är en normal till tangenten. Om 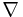f(P0) inte är parallell med 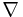g(P0) så har 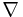f(P0) en projicerad vektor, v, som inte är en nollvektor längs tangenten till C i P0. Det innebär att f har en positiv riktningsderivata i P0 i vs riktning och en negativ riktningsderivata i motsatt riktning till v. Därmed ökar f om den rör sig bort från P0 i riktningen v och minskar i riktningen -v, vilket i sin tur innebär att f inte kan ha ett lokalt maximum eller minimum i P0. 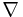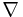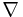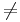Det innebär att f(P0) måste vara parallell med g(P0) och eftersom g(P0) 0 så måste det finnas ett tal, λ0, sådant att 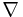f(P0) = -λ0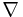g(P0) eller
Båda komponenterna i ovanstående vektor försäkrar oss om att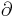 
L/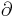x = 0 och att 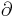L/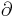y = 0 i (x0,y0,λ0). Den tredje ekvationen som måste satisfieras av en stationär punkt på L är 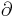L/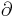λ = g(x,y) = 0. Den satisfieras i punkten (x0,yo,λ0) därför att P0 ligger på C. Då fås att (x0,yo,λ0) är en stationär punkt till L(x,y,λ).
Exempel
Maximera f(x,y) = x3y5 under bivillkoret g(x,y) = x + y = 8
Lösning
Vi börjar med att ställa upp lagrangefunktionen
L(x,y,λ) = x3y5 + λ(x + y - 8)
Vi tar sedan fram alla partiella derivator och sätter dem lika med noll i ett ekvationssystem
A: 3x2y5 + λ = 0 B: 5x3y4 + λ = 0 C: x + y - 8 = 0
A - B ger
C: x + y - 8 = 0 D: 3x2y5 - 5x3y4 = 0-5x + 3y = 0
Detta ger
x = 3 y = 5.
Det sökta värdet ges av f(3,5) = 84375.
Källa
Calculus, A Complete Course 4th Edition av Robert A. Adams
