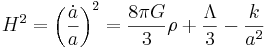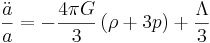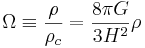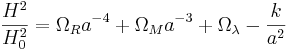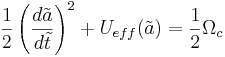Från Rilpedia

Friedmanns ekvationer relaterar olika kosmologiska parametrar inom ramen för den allmänna relativitetsteorin. De härleddes av Alexander Friedmann år 1922 från Einsteins fältekvationer under vissa symmetriantaganden lämpliga för en kosmologisk modell. Från dessa ekvationer härleddes Friedmann-Lemaître-Robertson-Walkermetriken för en fluid med en given densitet och tryck. Ekvationerna är:

där ρ och p är densiten och trycket hos fluiden, Λ är den kosmologiska konstanten som möjligen kan förklaras av vakuumenergin, G är gravitationskonstanten, k ger universums krökning, och a är skalfaktorn. I dessa ekvationer sätts c till värdet 1 och skulle annars finnas med i ekvationerna. Hubbleparametern H är expansionshastigheten hos universum, ett värde som kan ändras med tiden om andra delar av ekvationen är tidsberoende särskilt energidensiteten, vakuumenergin och krökningen. En bestämning av Hubbleparameterns värde nu ger Hubblekonstanten, som är proportionalitetsfaktorn i Hubbles lag. Tillämpad på en fluid med en given tillståndsekvation ger Friedmanns ekvationer utvecklingen i tiden och geometrin hos universum som en funktion av fluiddensiteten.

Vissa kosmologer kallar den andra av de båda ekvationerna för accelerationsekvationen och reserverar begreppet Friedmanns ekvation för den första av ekvationerna.

Densitetsparametern

Den första av Friedmanns ekvationer definierar en densitetsparameter som är användbar för att jämföra olika kosmologiska modeller:

Denna term användes ursprungligen till att bestämma universums geometri och där ρ_c är den kritiska densitet då universum är platt. Om vakuumenergins densitet är noll och Ω är större än 1 så är geometrin sluten. Om Ω är mindre än 1 så är universum öppet. Emellertid kan man också inkludera krökningen och vakuumenergin i ett mer generaliserat uttryck för Ω så att denna energidensitetsparameter blir exakt 1. Då handlar det om att mäta de olika komponenterna som vanligtvis markeras med olika indices. Enligt Lambda-CDM modellen är de viktiga komponenterna hos Ω baryoner, kall mörk materia och mörk energi. Rumtidens geometri är i det allra nämraste helt platt enligt mätningar som gjorts sonden WMAP vilket betyder att krökningsparametern κ är noll.

Den första av Friedmanns ekvationer skrivs ofta i en form med densitetsparametrar.

Här är Ω_R är densitetsparameterna för strålning, Ω_M är densitetsparameterna för materia (mörk materia plus baryonisk materia) och Ω_λ är den kosmologiska konstanten eller densiteten för vakuumenergin.

Friedmanns ekvation med annan skala

Sätt a=ãa₀, ρ_c=3H₀²/8π, ρ=ρ_cΩ, , Ω_c=-κ/H₀²a₀² där a₀ och H₀ är dagens värde på skalfaktorn respektive Hubbleparametern. Då får vi

där U_eff(ã)=Oã²/2. För varje form av den effektiva potentialen U_eff(ã), finns det en tillståndsekvation p=p(ρ) som ger ekvationen.

Referens

• L. Bergström & A. Goobar; Cosmology and Particle Astrophysics, 2:nd ed, Springer (2004). ISBN 3-540-43128-4