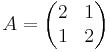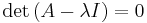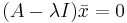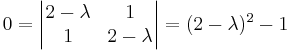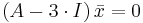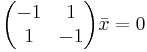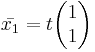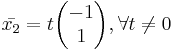Egenvärde, egenvektor
Från Rilpedia
Innehåll |
Definition
Matematiskt definieras egenvektorer och egenvärden på följande sätt:
Låt F vara en linjär avbildning på ett linjärt rum V. En vektor u skild från nollvektorn i V sådan att
- F(u) = λu
för något tal λ kallas en egenvektor till F med egenvärdet λ.
Om vi framställer F som en matris A, så kan vi med hjälp av matriser skriva
- A·U = λ·U,
där matrisen U kan vara en koordinatvektor.
Tolkningar
Den geometriska tolkningen av en egenvektor kan sägas vara att en egenvektor är en avbildning på sig själv och egenvärdet bestämmer skalan för denna avbildning.
En linjärtransformation i rummet, (t.ex. rotation, reflektion, töjning, kompression (matematik), skjuvning eller någon kombination av dessa, kan visualiseras av den effekt de ger på vektorer i rummet. Vektorer kan i detta fall visualiseras som pilar som går från en punkt i rummet till en annan.
Egenskaper
- En egenvektor av en linjärtransformation är en vektor som antingen förblir opåverkad, eller endast multipliceras med en skalär faktor i och med transformationen. (Att den förblir opåverkad skulle motsvara att den multiplicerats med en skalär faktor lika med 1).
- Egenvärdet av en (ej nollvärd) egenvektor är skalärfaktorn som den (egenvektorn) har multiplicerats med.
- Ett egenvärde av en linjärtransformation är en faktor för vilken det finns en (ej nollvärd) egenvektor som har denna faktor som sitt egenvärde.
- Egenrummet till ett egenvärde av en linjärtransformation är det vektorrum av alla egenvektorer till linjärtransformationen som har detta egenvärde.
- Den algebraiska multipliciteten av ett egenvärde är multipliciten för egenvärdet i sekularekvationen.
- Den geometriska multipliciteten av ett egenvärde är dimensionen av det tillhörande egenrummet.
- Spektrat av en transformation på ett ändligdimensionellt vektorrum är mängden av alla dess egenvärden. (I det oändligdimensionella fallet är konceptet med spektrum mer subtilt och beror av topologin hos vektorrummet.)
Exempel och lösningsmetoder
Låt oss anta att vi har en 2x2 matris A enligt
För att finna egenvärdena måste vi använda oss av sekularekvationen
och denna behövs nu för att kunna lösa den homogena ekvationen
"det" i sekularekvationen överst står för determinant.
Med hjälp av sekularekvationen får vi fram följande
och då med hjälp av i det här fallet en enkel andragradsekvation så får vi fram följande egenvärden
- λ1 = 3 och λ2 = 1
stoppar vi in de nu givna egenvärdena i homogena ekvationen (ovan) så får vi följande uppställningar. (vi räknar bara med det ena fallet här)
i mer utskriven matrisform är detta detsamma som
Nu tar vi hjälp av någon slags elimineringsmetod, ex) Gausselimination så får vi fram egenvektorerna (dvs det som x nu står för) vilket är
I det andra fallet när λ2 = 1 får vi följande egenvektor
Tillämpningar
Egenvärdesproblem har varit en viktig del inom matematiken och dess tillämpningar under mer än tvåhundra år. Inom mekaniken ger egenvärden resonansfrekvenser för mekaniska system. De grundtoner som frambringas av till exempel stränginstrument motsvaras av egenvärden för den svängande strängen. Inom kvantmekaniken är egenvärden av fundamental betydelse. De bestämmer till exempel de möjliga energinivåerna hos atomer och molekyler.
Matematiskt har egenvärdena och egenvektorerna betydelse vid diagonalisering av matriser och i det allmänare fallet Jordans normalform.
Se även