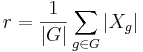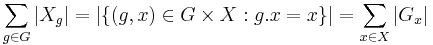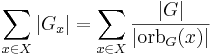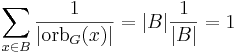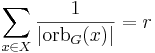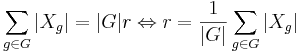Burnsides lemma

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Burnsides lemma, även kallat Cauchy-Frobenius lemma, är ett resultat inom gruppteori.

Låt G vara en ändlig grupp som verkar på en mängd X, och för varje g i G, låt $X g$ beteckna fixpunktsmängden till g. Burnsides lemma säger då att antalet banor, r, är

$r=\frac{1}{|G|}\sum_{g \in G} |X_g|$

med andra ord är antalet banor lika med det aritmetiska medelvärdet av storleken på fixpunktsmängderna.

Bevis

För att bevisa satsen kan man först notera att

$\sum_{g \in G} |X_g| = | \{ (g,x) \in G \times X: g.x = x \} | = \sum_{x \in X} |G_x|$

där g.x beskriver att g verkar på x och $G x$ är stabilisatorn till x. Storleken av $G x$ är storleken av G delat på storleken av x:s bana:

$\sum_{x \in X} |G_x| = \sum_{x \in X} \frac{|G|}{|\operatorname{orb}_G(x)|}$

om man väljer en godtycklig bana, B, i X, får man att summan

$\sum_{x \in B} \frac{1}{|\operatorname{orb}_G(x)|} = |B| \frac{1}{|B|} = 1$

för alla banor får man då att:

$\sum_{x \in X} \frac{1}{|\operatorname{orb}_G(x)|} = r$

där r är antalet banor. Detta ger, med föregående uträkningar, att:

$\sum_{g \in G} |X_g| = |G|r \Leftrightarrow r = \frac{1}{|G|} \sum_{g \in G} |X_g|$

vilket skulle visas.

Tillämpning

Burnsides lemma kan användas då man vill beräkna antalet färgningar av en geometrisk figur då man anser att två färgningar är ekvivalenta om den ena kan fås från den andra genom ett antal rotationer och/eller speglingar.

Historia

William Burnside bevisade lemmat i sin bok Theory of Groups of Finite Order från 1897, men angav Georg Frobenius som upphovsman, dock var lemmat känt redan för Augustin Louis Cauchy 1845. Därför kallas ibland lemmat för "lemmat som inte är Burnsides".

Burnsides lemma

Från Rilpedia

Bevis

Tillämpning

Historia

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk