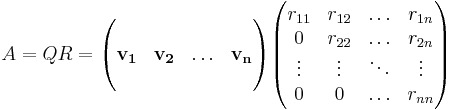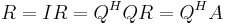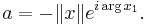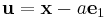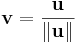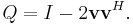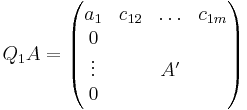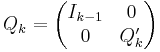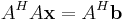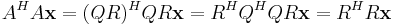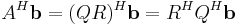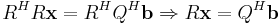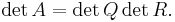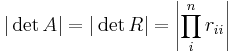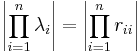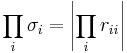QR-faktorisering

Från Rilpedia

Version från den 19 mars 2009 kl. 22.58 av Calle (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom linjär algebra är QR-faktorisering en matrisfaktorisering av en (reell) matris i en ortogonal matris och en triangulär matris.

Innehåll

Definition

En QR-faktorisering av en reell kvadratisk matris A kan uttryckas:

A = QR

För en ortogonal matris Q och en uppåt triangulär matris R. Om A istället är komplex är Q en unitär matris.

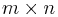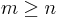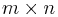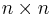Detta kan generaliseras till att A är en matris av format m \times n där m \geq n , då Q är en ortogonal (unitär) matris med format m \times n och R är en uppåt triangulär matris med format n \times n .

Beräkning

Det finns flera sätt att beräkna QR-faktoriseringen av en matris. Det vanligaste sättet är genom Gram-Schmidts ortogonaliseringsprocess.

Genom Gram-Schmidt

Om matrisen A har kolonnvektorerna 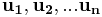\mathbf{u_1}, \mathbf{u_2}, ... \mathbf{u_n} som är linjärt oberoende, kan man genom Gram-Schmidts ortogonaliseringsprocess bestämma vektorer 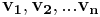\mathbf{v_1}, \mathbf{v_2}, ... \mathbf{v_n} som är ortogonala. De gamla 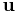\mathbf{u} -vektorerna kan nu skrivas som linjärkombinationer av de nya 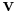\mathbf{v} -vektorerna:

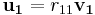
\mathbf{u_1} = r_{11}\mathbf{v_1}
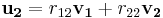
\mathbf{u_2} = r_{12}\mathbf{v_1} + r_{22}\mathbf{v_2}
...
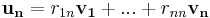
\mathbf{u_n} = r_{1n}\mathbf{v_1} + ... + r_{nn}\mathbf{v_n}

Om vi nu placerar våra r-värden i en matris, R, och de ortogonala vektorerna i en annan matris, Q, kan vi uttrycka den gamla matrisen A som produkten av dessa:

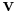A = QR = \begin{pmatrix} & & & \\ \mathbf{v_1} & \mathbf{v_2} & \ldots & \mathbf{v_n} \\ & & & \end{pmatrix} \begin{pmatrix} r_{11} & r_{12} & \ldots & r_{1n} \\ 0 & r_{22} & \ldots & r_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & r_{nn} \end{pmatrix}

Då \mathbf{v} -vektorerna är ortogonala är Q ortogonal (unitär om vektorerna är komplexa).

För att få r-värdena kan man lösa dem ur ortogonaliseringsprocessen man gör, eller så använder man sig av faktumet att:

R = IR = Q^HQR = Q^HA \,

Så att R kan beräknas genom en enkel matrismultiplikation (QH står för det hermiteska konjugatet till Q, som i det reella fallet är samma sak som transponat).

Med Householderreflektioner

En Householdertransformation är en linjär avbildning som reflekterar en vektor i ett hyperplan. Detta kan användas till att QR-faktorisera en matris. Denna metod är numeriskt stabilare än Gram-Schmidt-metoden och har en tidskomplexitet på O(n3).

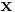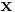För beräkningen tas speciella Householdertransformationer fram. Man utgår från en vektor \mathbf{x} och tar ett tal a så att \|\mathbf{x}\| = |a| . Om QR-faktoriseringen görs med flyttalsberäkningar och vektorn är reell bör a väljas med motsatt tecken från första elementet i vektorn \mathbf{x} , om vektorn är komplex bör a väljas genom:

a = -\|x\|e^{i \arg x_1}.

Sedan konstrueras Householdertransformationen Q på följande sätt (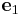\mathbf{e}_1 är vektorn (1,0,...,0)T):

\mathbf{u} = \mathbf{x} - a\mathbf{e}_1
\mathbf{v} = \frac{\mathbf{u}}{\| \mathbf{u} \|}
Q = I - 2\mathbf{vv}^H.

För att QR-faktorisera m×n-matrisen A, konstruerar man en Householdertransformation Q1 enligt ovan från första kolonnen i A. Man får då

Q_1 A = \begin{pmatrix} a_1 & c_{12} & \ldots & c_{1m} \\ 0 \\ \vdots & & A' \\ 0 \end{pmatrix}

Man kan sedan konstruera en ny Householdertransformation Q2' från första kolonnen i A' (A' fås genom att plocka bort första kolonnen och första raden i Q1A). Eftersom man vill verka på matrisen Q1A och inte A' så tar man matrisen Q2' och fyller ut den. För ett generellt steg i QR-faktoriseringen får man matrisen:

Q_k = \begin{pmatrix} I_{k-1} & 0 \\ 0 & Q_k' \end{pmatrix}

Vid multiplikation med Q2 fås alltså en matris Q2Q1A som är lika stor som A. Ur denna matris läser man ut A'' som är två steg mindre än A, tar den första kolonnen och konstruerar Q3' varur man konstruerar Q3 enligt ovan.

Sedan upprepas detta k = min(m − 1,n) steg, då man fått

R = QkQk − 1...Q1A

där R är uppåt triangulär och

Q = Q1Q2...Qk

är en unitär matris (eftersom Householdertransformationer är unitära). Alltså är A = QR en QR-faktorisering av A.

Tillämpningar

Minsta kvadrat-lösningar

Om man ska hitta minsta kvadrat-lösningen till ett ekvationssystem givet av ekvationen 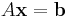A\mathbf{x} = \mathbf{b} förenklas detta om A är QR-faktoriserad. Lösningen ges i vanliga fall av

A^HA\mathbf{x} = A^H\mathbf{b}

Om A = QR ger vänsterledet

A^HA\mathbf{x} = (QR)^HQR\mathbf{x} = R^HQ^HQR\mathbf{x} = R^HR\mathbf{x}

och högerledet

A^H\mathbf{b} = (QR)^H\mathbf{b} = R^HQ^H\mathbf{b}

så att ekvationen blir

R^HR\mathbf{x} = R^HQ^H\mathbf{b} \Rightarrow R\mathbf{x} = Q^H\mathbf{b}

som är ett väldigt lättlöst ekvationsysstem eftersom R är triangulär.

Determinanter, egenvärden och singulärvärden

Om A är en kvadratisk matris av storlek n som är QR-faktoriserad, A = QR, då det ur räknelagarna för determinanten att

\det A = \det Q \det R.\,

Eftersom Q är unitär är | detQ | = 1, vilket ger:

|\det A|=|\det R| = \left| \prod_{i}^n r_{ii} \right|

där rii är värdena i R:s diagonal. Då man även vet att determinanten av A är produkten av A:s egenvärden följer det att

\left| \prod_{i=1}^n \lambda_i \right| = \left| \prod_{i=1}^n r_{ii} \right|

där λi är A:s egenvärden.

Man kan generalisera resonemanget ovan till att gälla matriser A som inte är kvadratiska, då man från egenskaper hos singulärvärdesfaktoriseringen får att:

\prod_{i} \sigma_i = \left| \prod_{i} r_{ii} \right|

där σi är A:s singulärvärden.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/QR-faktorisering"
Personliga verktyg