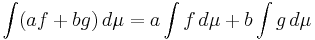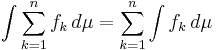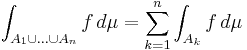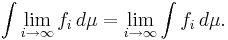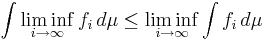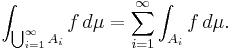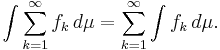Egenskaper hos måttintegral
Från Rilpedia
- Denna artikel utgör en fördjupning av artikeln om måttintegral.
Måttintegraler har några intressanta egenskaper. Låt 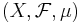 vara ett måttrum,
vara ett måttrum, 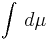 vara ett måttintegral med avseende på måttet µ och f och g vara mätbara funktioner
vara ett måttintegral med avseende på måttet µ och f och g vara mätbara funktioner 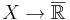 .
.
Innehåll |
Grundläggande egenskaper
Måttintegraler dessa grundläggande egenskaper.
Monotonicitet: om 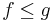 så är
så är
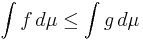 .
.
Linjäritet: om f och g är integrerbara så är summan 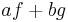 också integrerbar och
också integrerbar och
för alla 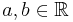 .
.
Triangelolikheten för integraler: absolutbeloppet av integralen är mindre än integralen av absolutbeloppet:
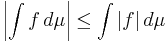 .
.
Additivitet för funktioner: om 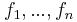 är integrerbara funktioner så är
är integrerbara funktioner så är
Additivitet för mängder: om 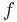 är mäbara funktionen och
är mäbara funktionen och 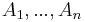 är parvis disjunkta mätbara mängder så är
är parvis disjunkta mätbara mängder så är
Nollmängder
Nollmängder påverkar inte måttintegraler.
- Om
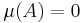 så är
så är
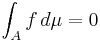 .
.
- Om
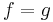 µ-nästan överallt så är
µ-nästan överallt så är
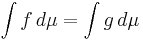 .
.
Konvergenssatser
Måttintegraler har många konvergenssatser. Konvergenssatser kallas de villkor som leder till
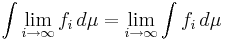 ,
,
där 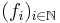 är integrerbara funktioner för alla
är integrerbara funktioner för alla 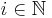 , så att det finns
, så att det finns
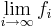 .
.
Med andra ord är en konvergenssats ett tillräckligt villkor för att man ska kunna byta ordning på gränsvärde och integral.
Monotona konvergenssatsen: om 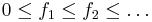 så existerar gränsvärdet
så existerar gränsvärdet 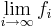 och
och
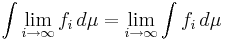 .
.
Dominerade konvergenssatsen: om det finns en funktion g som är integrerbar så att 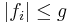 för alla
för alla 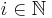 nästan överallt och
nästan överallt och 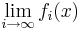 existerar så är
existerar så är
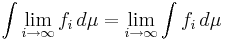 .
.
Begränsade konvergenssatsen: om 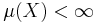 och
och 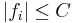 för alla
för alla 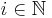 var
var  så är
så är
Fatous lemma: om 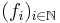 är mätbara funktioner så gäller att
är mätbara funktioner så gäller att
och
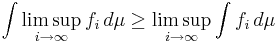 .
.
Sigma-additivitet
Måttintegralen av icke-negativa funktioner är sigma-additiv över mängder. Det vill säga om 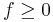 och
och 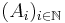 är uppräknelig sekvens av parvis disjunkta mängder i
är uppräknelig sekvens av parvis disjunkta mängder i 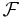 så är
så är
Detta betyder också att funktionen 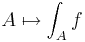 , där
, där 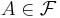 , är ett mått eftersom integralen över tomma mängden är noll.
, är ett mått eftersom integralen över tomma mängden är noll.
Måttintegralen är också sigma-additiv med avseende på icke-negativa funktioner. Den här egenskapen kallas Beppo Levis sats: om 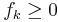 är uppräknelig sekvens av mätbara funktioner så är
är uppräknelig sekvens av mätbara funktioner så är
Detta är en enkel följd av monotona konvergenssatsen, som kan appliceras på alla delsummor av de oändliga summorna.
Se även
Källor
- G.B. Folland, Real analysis: Modern techniques and their applications, Second edition, Wiley interscience, (1999)