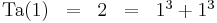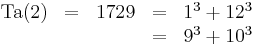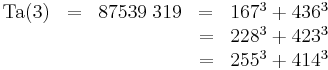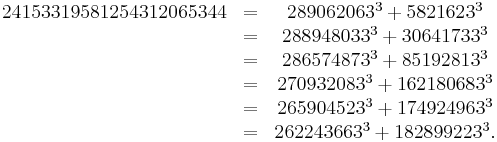Taxital

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom talteorin är det n-te taxitalet det minsta positiva heltal som kan uttryckas som summan av två positiva kuber på n olika sätt. Det n-te taxitalet betecknas ofta Ta(n) eller Taxicab(n).

G. H. Hardy och E. M. Wright bevisade 1954 att Ta(n) existerar för alla positiva heltal n, men deras bevis var inte konstuktivt, det vill säga det hjälper oss inte att finna nya taxital. Det enda taxital som man hittills känner till är de följande fem (talföljd A011541 i OEIS):

\begin{matrix}\operatorname{Ta}(1)&=&2&=&1^3 + 1^3\end{matrix}
\begin{matrix}\operatorname{Ta}(2)&=&1729&=&1^3 + 12^3 \\&&&=&9^3 + 10^3\end{matrix}
\begin{matrix}\operatorname{Ta}(3)&=&87539\;319&=&167^3 + 436^3 \\&&&=&228^3 + 423^3 \\&&&=&255^3 + 414^3\end{matrix}
\begin{matrix}\operatorname{Ta}(4)&=&6963472309248&=&2421^3 + 19083^3 \\&&&=&5436^3 + 18948^3 \\&&&=&10200^3 + 18072^3 \\&&&=&13322^3 + 16630^3\end{matrix}
\begin{matrix}\operatorname{Ta}(5)&=&48988659276962496&=&38787^3 + 365757^3 \\&&&=&107839^3 + 362753^3 \\&&&=&205292^3 + 342952^3 \\&&&=&221424^3 + 336588^3 \\&&&=&231518^3 + 331954^3\end{matrix}

Man vet inte exakt hur stort Ta(6) är, men det är inte större än 24 153 319 581 254 312 065 344, eftersom

\begin{matrix}24153319581254312065344 &=&289062063^3 + 5821623^3 \\ &=&288948033^3 + 30641733^3 \\ &=&286574873^3 + 85192813^3 \\ &=&270932083^3 + 162180683^3 \\ &=&265904523^3 + 174924963^3 \\ &=&262243663^3 + 182899223^3. \end{matrix}

Det är också känt att Ta(6) > 68 000 000 000 000 000 000.

Hämtad från "https://sv.rilpedia.org/wiki/Taxital"
Personliga verktyg