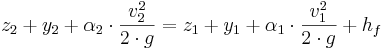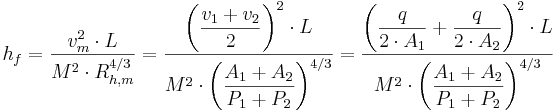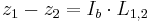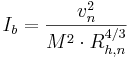Direkt stegmetod

Från Rilpedia

Texten från svenska Wikipedia

Den direkta stegmetoden är en beräkningsmetod för att beräkna vattenytans lutning i långa homogena kanaler och öppna diken, där det inte råder något naturligt vattendjup. Metoden bygger på energiekvationen och Mannings formel.

$z_2 +y_2 + \alpha_2 \cdot \dfrac {v_2^2}{2 \cdot g} = z_1 +y_1 + \alpha_1 \cdot \dfrac {v_1^2}{2 \cdot g} + h_f$

där

z = Höjd i ett referenssystem (-)

y = Verkligt vattendjup (m)

α = Korrektionsfaktor för kinetisk energi (-)

v = Hastighet (m/s)

g = Tyngdaccelerationen (m/s²)

h_f = Strömningsförlust (meter vattenpelare)

Den sista delen i ekvationen ovan (h_f) är höjdförlusten mellan punkt 1 och punkt 2. Höjdförlusten beräknas med Mannings formel och skrivs:

$h_f = \dfrac {v_m^2 \cdot L}{M^2 \cdot R_{h,m}^{4/3}} = \dfrac {\left( \dfrac {v_1 +v_2}{2} \right)^2 \cdot L}{M^2 \cdot \left( \dfrac {A_1 + A_2}{P_1 +P_2} \right)^{4/3}} = \dfrac {\left( \dfrac {q}{2\cdot A_1} + \dfrac {q}{2 \cdot A_2} \right)^2 \cdot L}{M^2 \cdot \left( \dfrac {A_1 + A_2}{P_1 +P_2} \right)^{4/3}}$

där

h_f = Strömningsförlust (meter vattenpelare)

v_m = Medelhastigheten mellan punkt 1 och punkt 2 (m/s)

L = Horisontalt avstånd mellan punkt 1 och punkt 2 (m)

M = Mannings tal (m^1/3/s)

R_h,m = Genomsnittlig hydraulisk radie mellan punkt 1 och punkt 2 (m)

A = Våt tvärsnitsarea (m²)

P = Våt perimeter (m)

q = Flöde (m³)

När den undersökta kanalen eller öppna diket är homogen över en längre sträcka, gäller följande samband:

$z_1 - z_2 = I_b \cdot L_{1,2}$

där

z = Höjd i ett referenssystem (-)

I_b = Bottenlutning (-)

L_1,2 = Horisontalt avstånd mellan punkt 1 och punkt 2 (m)

Dessutom gäller att:

α 1 = α2 = α

α = Korrektionsfaktor för kinetisk energi (-)

Bottenlutningen kan med hjälp av Mannings formel även skrivas på följande sätt:

$I_b = \dfrac {v_n^2}{M^2 \cdot R_{h,n}^{4/3}}$

där

I_b = Bottenlutning (-)

v_n = Naturlig medelhastighet (m/s)

M = Mannings tal (m^1/3/s)

R_h,n = Hydraulisk radie vid naturligt vattendjup (m)

Om alla ovanstående uttryck kombineras och omgrupperas på lämpligt sätt, så erhålls följande samband:

$L_{1,2} \cdot \left( \dfrac {v_m^2}{M^2 \cdot R_{h,m}^{4/3}} - \dfrac {v_n^2}{M^2 \cdot R_{h,n}^{4/3}} \right) = \left( y_2 + \alpha \cdot \dfrac {v_2^2}{2 \cdot g} \right) - \left( y_1 + \alpha \cdot \dfrac {v_1^2}{2 \cdot g} \right)$

och

$L_{1,2} = \dfrac {\left( y_2 + \alpha \cdot \dfrac {v_2^2}{2 \cdot g} \right) - \left( y_1 + \alpha \cdot \dfrac {v_1^2}{2 \cdot g} \right)}{\left( \dfrac {v_m^2}{M^2 \cdot R_{h,m}^{4/3}} - \dfrac {v_n^2}{M^2 \cdot R_{h,n}^{4/3}} \right)} = \dfrac {\left( y_2 + \alpha \cdot \dfrac {q^2}{2 \cdot A_2^2 \cdot g} \right) - \left( y_1 + \alpha \cdot \dfrac {q^2}{2 \cdot A_1^2 \cdot g} \right)}{\left( \dfrac {q^2}{M^2 \cdot A_m \cdot R_{h,m}^{4/3}} - \dfrac {q^2}{M^2 \cdot A_n \cdot R_{h,n}^{4/3}} \right)}$

där

L_1,2 = Horisontalt avstånd mellan punkt 1 och punkt 2 (m)

v_m = Medelhastigheten mellan punkt 1 och punkt 2 (m/s)

M = Mannings tal (m^1/3/s)

R_h,m = Genomsnittlig hydraulisk radie mellan punkt 1 och punkt 2 (m)

v_n = Naturlig medelhastighet (m/s)

R_h,n = Hydraulisk radie vid naturligt vattendjup (m)

y = Verkligt vattendjup (m)

α = Korrektionsfaktor för kinetisk energi (-)

v = Hastighet (m/s)

g = Tyngdaccelerationen (m/s²)

q = Flöde (m³)

A = Våt tvärsnittsarea (m²)

A_m = Genomsnittlig våt tvärsnittsarea mellan punkt 1 och punkt 2 (m²)

A_n = Våt tvärsnittsarea vid naturligt vattendjup (m²)

Om flödet (q), Mannings tal (M) och kanalprofilen är kända, liksom det verkliga vattendjupet vid en punkt 1 (y₁), kan avståndet uppströms (L_1,2 > 0) eller nerströms (L_1,2 < 0) lätt beräknas där vattendjupet (y₂) råder. Man sätter alltså ett lämpligt värde på y₂ och ser var y₂ inträffar. Nu när man vet var punkt 2 hamnar, kan man gå vidare att beräkna avståndet till punkt 3 (L_2,3), där vi har djupet y₃ och så vidare.

Genom att välja små steg mellan vattendjupsförändringarna, kan detaljerade vattenyteprofiler skapas över långa sträckor av kanalen eller öppna diket. Då kan man t.ex. beräkna hur långt uppströms en fördäming påverkar vattenståndet i en kanal eller öppet dike.

Tillämpningsområde

Den direkta stegmetoden fungerar bra när flödet är känt och strömningstillståndet antingen är subkritisk eller superkritisk. Däremot fungerar inte den direkta stegmetoden när det finns någon kritisk strömning i den aktuella delen av kanalen eller öppna diket.

Den direkta stegmedoden passar bättre för långa homogena kanaler och öppna diken än stegmetoden (som passar bättre i mer naturliga vattendrag).

Se även

Direkt stegmetod

Från Rilpedia

Tillämpningsområde

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda