Från Rilpedia

Välordningssatsen är en sats inom mängdteorin som säger att varje mängd kan välordnas. Givet mängdlärans övriga axiom är välordningssatsen ekvivalent med urvalsaxiomet.

Bevis med hjälp av Zorns lemma

Låt X vara en mängd, och låt U vara mängden av partiella välordningar på X, dvs välordningar av någon delmängd till X. Inklusionsrelationen ger en partiell ordning på U. Eftersom unionen av välordningar är en välordning har varje kedja i U en övre gräns, så enligt Zorns lemma finns ett maximalt element E i U. Om det finns något element x i X som inte ligger i definitionsområdet för E så kan E utvidgas genom att placera x första, vilket motsäger maximaliteten för E. Därmed är E en välordning på X.

Bevis med hjälp av urvalsaxiomet

Låt X vara en mängd, och låt f vara en urvalsfunktion på potensmängden till X. Definiera rekursivt en funktion g från ORD till X genom

g(0) = f(X)

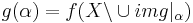
Låt nu x < y omm g(x) < g(y)