Från Rilpedia

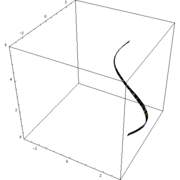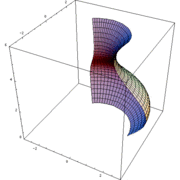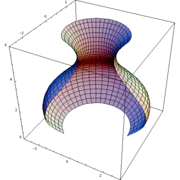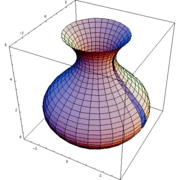
En rotationskropp är i matematiken den volym som innesluts av kurvan när den roterar kring en axel. Ett exempel på ett fysiskt objekt som har formen av en rotationskropp är vad som helst som svarvats eller drejats, exempelvis en skål eller ett basebollträ. I teorin kan en rotationskropp vara oändligt lång men ändå ha ändlig volym, men fysiska rotationskroppar har naturligtvis begränsad längd.

Volymen av en rotationskropp beräknas som integralen av rotationskroppens snittyta från dess början till dess slut. Denna är lika med funktionsvärdet i kvadrat gånger pi (och motsvarar cirkelns area som funktion av dess radie).

Volymen 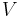av rotationskroppen av 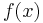mellan A och B, roterad runt x-axeln, är alltså

Volymen 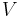av rotationskroppen av 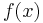mellan A och B, roterad runt y-axeln, är