Betingad konvergens

Från Rilpedia

(Omdirigerad från Riemanns omordningssats)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

I matematiken sägs en serie 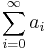$\sum_{i=0}^\infty a_i$ vara betingat konvergent om den är konvergent, det vill säga gränsvärdet

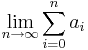$\lim_{n\rightarrow\infty} \sum_{i=0}^n a_i$ existerar, men att serien inte är absolutkonvergent, det vill säga att 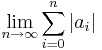$\lim_{n\rightarrow\infty} \sum_{i=0}^n |a_i |$ inte är konvergent.

Exempel

Serien 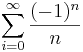$\sum_{i=0}^\infty \frac{(-1)^n}{n}$ är betingat konvergent.

Mer allmänt, så säger Leibniz kriterium om betingad konvergens att om 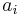$\,a_i$ är en strängt avtagande följd av positiva reella tal, så är serien 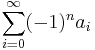$\sum_{i=0}^\infty (-1)^n a_i$ konvergent. En sådan serie är emellertid i allmänhet inte absolutkonvergent.

Riemanns omordningssats

En grundläggande sats i matematisk analys säger att gränsvärdet för en absolutkonvergent serie inte ändras om man ändrar ordningen på termerna i serien. För betingat konvergenta serier är situationen den motsatta:

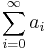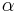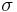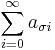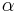Teorem: Låt $\sum_{i=0}^\infty a_i$ vara betingat konvergent, och låt $\,\alpha$ vara ett reeelt tal. Då finns en permutation $\,\sigma$ av de naturliga talen sådan att serien $\sum_{i=0}^\infty a_{\sigma i}$ konvergerar mot $\,\alpha$ .