Partition av en mängd

Från Rilpedia

Texten från svenska Wikipedia

Partitionering av en mängd (hela cirkeln) i sex olika delar (de färgade områdena).

För andra betydelser, se partition.

En partition av en mängd är en uppdelning av av mängden i delar som inte överlappar, men som tillsammans inte ger "hål" jämfört med den ursprungliga mängden.

Formell definition

En partition av en mängd M är en mängd som består av icketomma delmängder till M sådan att ett element i M finns i exakt en av dessa delmängder.

Detta kan formuleras ekvivalent som att P är en partition av M om:

• Unionen av alla element i P är lika med M (P täcker M).
• Varje snitt av två element i P är tomt. (Elementen i P är disjunkta).

Detta kan skrivas symboliskt:

• 
• .

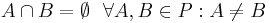Notera alltså att elementen i P inte kallas partitioner, utan P kallas partition.

Exempel

• En mängd innehållande ett element, {x} kan partitioneras på ett sätt: {{x}}.
• En partitionering av {1,2,3} är {{1},{2,3}}, en annan är {{1,2},{3}}.
• Låt Z vara mängden av alla heltal, J alla jämna tal och U alla udda tal. Då är {J, U} en partition av Z.
• Låt Z⁺ vara alla positiva tal och Z^- alla negativa tal. Då är {{0}, Z⁺, Z^-} en partition av Z.

Antal partitioner

Belltalen, B_n är antalet möjliga partitioner av en mängd med n element. Likaså är Stirlingtalen av andra slaget, S(n,k) antalet möjliga partitioner av en mängd med n element i k olika delar.