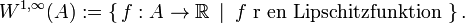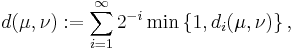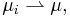Metrik av mått
Från Rilpedia
Metrik av mått är en metrik mellan mått. Metrik av mått är en viktig struktur när man undersöker svag konvergens av mått.
Innehåll |
Definitioner
Först behövs några definitioner för metriken.
Mängden av Radonmått är mängden av alla Radonmått i 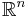 begränsade till Borelmängder
begränsade till Borelmängder 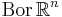 :
:
Mängden av Lipschitzfunktioner är mängden av alla Lipschitzfunktioner definierad i en mängd 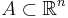 (se också
(se också 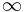 -Sobolevrummet):
-Sobolevrummet):
i-klass metriken av Radonmått, där 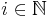 , är en funktion
, är en funktion 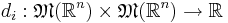 definierad som:
definierad som:
dvs supremum av distansen för måttintegraler av mått 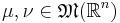 över Lipschitzfunktioner i bollen
över Lipschitzfunktioner i bollen 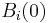 .
.
Det går att visa att  är ett metriskt rum för alla
är ett metriskt rum för alla 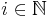 . Tyvärr det är inte ett fullständigt metriskt rum. Så istället definierar man en annan metrik med hjälp av metrikerna
. Tyvärr det är inte ett fullständigt metriskt rum. Så istället definierar man en annan metrik med hjälp av metrikerna 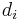 ,
, 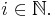
Formell definition
Metrik av mått, 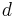 , är en formellt funktion
, är en formellt funktion 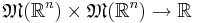 definierad som:
definierad som:
för 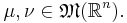
Det går att visa att rummet 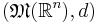 , rummet av mått, är ett fullständigt metriskt rum och dessutom separabelt. Den täta och uppräkneliga delmängden av Radonmått i
, rummet av mått, är ett fullständigt metriskt rum och dessutom separabelt. Den täta och uppräkneliga delmängden av Radonmått i 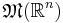 är summan av Diracmått över mittpunkter av dyadiska kuber i
är summan av Diracmått över mittpunkter av dyadiska kuber i  . [1]
. [1]
Svag konvergens av mått
Eftersom 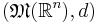 är ett metriskt rum man kan definiera konvergens av mått: en följd av mått
är ett metriskt rum man kan definiera konvergens av mått: en följd av mått  konvergera till
konvergera till 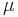 om
om
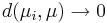 , när
, när 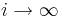 .
.
Man kallar den här typen av konvergens för svag konvergens av mått och skriver:
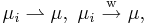 eller
eller 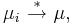
där w (eng. weak) och  (eng. star) antyder på svaga stjärnatopologin av Radonmått.
(eng. star) antyder på svaga stjärnatopologin av Radonmått.
Det går att visa att
om och endast om
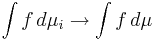 , när
, när 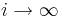 .
.
för alla 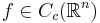 där
där 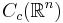 är mängden av alla kontinuerliga funktioner i
är mängden av alla kontinuerliga funktioner i 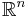 med kompakt stöd.
med kompakt stöd.
Anmärkning: det finns exempel av mängder 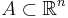 när
när  men
men 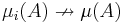 . Å andra sidan om
. Å andra sidan om 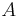 är begränsad och
är begränsad och 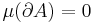 så är
så är 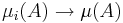 om
om  .
.
Se även
Referenser
- ↑ Pertti Mattila (1995), Geometry of Sets and Measures in Euclidean Spaces: Fractals and rectifiability (1st edition), Anmärkning 14.15, Cambridge University Press, ISBN 978-0-521-65595-8




![\mathfrak{M}(\R^n) := \left\{\, \mu : \mathrm{Bor} \, \R^n \to [0,\infty] \,\ | \,\ \mu \mbox{ är ett Radonmått } \right\}.\,](/w/images/sv.rilpedia.org/math/c/e/b/cebde1acddb4783a6e1fbb254aba230c.png)