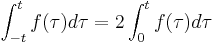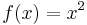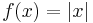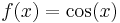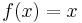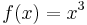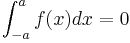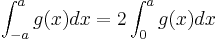Jämna och udda funktioner
Från Rilpedia
Jämna och udda funktioner är matematiska funktioner som uppfyller vissa symmetriska villkor.
Innehåll |
Jämn funktion
En jämn funktion har egenskapen f( − x) = f(x) för alla x, dvs dess graf är spegelsymmetrisk kring y-axeln. Om en jämn funktion har en derivata är den en udda funktion. En användbar egenskap hos jämna funktioner är att integralen över ett symmetriskt intervall kring noll är två gånger integralen av endast ena halvan:
Namnet motiveras bl.a. av att funktionerna xn för jämna n är jämna funktioner, samt av att maclaurinutvecklingen av en jämn funktion bara har termer med jämna exponenter i.
Exempel
Udda funktion
En funktion f är udda om den har egenskapen f( − x) = − f(x) för alla x. Detta innebär att dess graf är rotationssymmetrisk kring origo, dvs om grafen roteras 180 grader i xy-planet runt origo, så erhålls samma graf. En udda funktions derivata är, om den existerar, en jämn funktion. En trevlig egenskap hos udda funktioner är att om man integrerar dem över ett intervall [-a,a], så blir resultatet 0.
Namnet motiveras bl.a. av att funktionerna xn för udda n är udda funktioner, samt av att maclaurinutvecklingen av en en udda funktion bara har termer med udda exponenter i.
Exempel
Udda funktioner:
Egenskaper
- Den enda funktionen som är både jämna och udda är den konstanta funktionen f(x) = 0.
- Summan av en udda och en jämn funktion är varken udda eller jämn, såvida en av funktionerna inte är konstant noll.
- Summan av två udda funktioner är udda, och varje multipel av en udda funktion är udda.
- Summan av två jämna funktioner är jämna, och varje multipel av en jämn funktion är jämn.
- Produkten av både två udda eller två jämna funktioner är en jämn funktion.
- Kvoten av både två udda eller två jämna funktioner är jämn.
- Kvoten av en jämn och en udda funktion är udda.
- En sammansatt funktion av två udda funktioner är udda. En sammansättning av två jämna funktioner är jämn.
- En sammansatt funktion av en udda och en jämn funktion är udda.
- Derivatan av en jämn funktion är udda (förutsatt att funktionen är deriverbar).
- Derivatan av en udda funktion är jämn (förutsatt att funktionen är deriverbar).
- Integralen av en udda funktion från -a till a är noll, dvs om f är udda:
- Integralen av en jämn funktion från -a till a är två gånger integralen från noll till A, dvs om g är jämn: