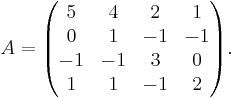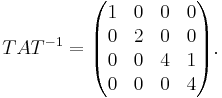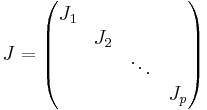Jordans normalform
Från Rilpedia
Jordans normalform är inom linjär algebra en form för matriser som visar att en matris M kan uttryckas som en "nästan diagonal" matris genom basbyte. Den "nästan diagonala" matrisen är en Jordanmatris med M:s egenvärden i diagonalen. Diagonalisering kan ses som ett specialfall av Jordans normalform.
Jordans normalform är uppkallad efter Camille Jordan.
Innehåll |
Bakgrund
En 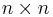 -matris A är diagonaliserbar om och endast om summan av egenrummens dimensioner är n, d.v.s. att dimensionen för varje egenrum till egenvärde λi, den geometriska multipliciteten är lika med den algebraiska multipliciteten för λi. Alla matriser är dock inte diagonaliserbara. Exempel:
-matris A är diagonaliserbar om och endast om summan av egenrummens dimensioner är n, d.v.s. att dimensionen för varje egenrum till egenvärde λi, den geometriska multipliciteten är lika med den algebraiska multipliciteten för λi. Alla matriser är dock inte diagonaliserbara. Exempel:
A:s egenvärden är 1, 2, 4, 4. Nollrummet N(A − 4I) är dock endast endimensionellt, så matrisen är inte diagonaliserbar. Jordans normalform är då den bästa formen, närmast diagonalform, med ettor på vissa positioner i superdiagonalen. Det finns en inverterbar matris T så att:
som är Jordanformen av A.
Generell beskrivning
Generellt kan en komplex matris A genom basbyte omvandlas till en Jordanmatris J, dvs en blockdiagonal matris
Där varje block Ji är ett Jordanblock på formen:
Matrisen J kallas A:s Jordanform.
- Diagonalelementen i J är A:s egenvärden.
- Ettorna i J säges ligga i superdiagonalen och symboliserar de platser som fyllts ut med generaliserade egenvektorer. Notera att platserna för ettor och nollor kan vara blandade längs J:s superdiagonal men varje J-block innehåller endast ettor i sin diagonal och säges vara en cykel av en viss längd. Olika cykler kan höra till samma egenvärde.
Härledning av Jordans normalform
Följande satser bygger upp varandra för att nå fram till Jordans normalform. Då bevisen är något långa utelämnas dessa förutom det för själva Jordans normalform.
Sats 1
Ett vektorrum V kan skrivas  där
där 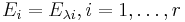 är generaliserade egenrummen till en avbildningsmatris
är generaliserade egenrummen till en avbildningsmatris 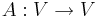
Sats 2
För ett generaliserat egenrum Ei gäller att dimEi = algebraiska multipliciteten för λi
Sats 3
Varje linjär avbildning 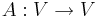 kan representeras av
kan representeras av 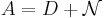 där D är en diagonalmatris och
där D är en diagonalmatris och 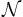 är en nilpotent matris. Det gäller även att D och
är en nilpotent matris. Det gäller även att D och 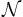 kommuterar, d.v.s. att
kommuterar, d.v.s. att 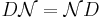
Definition: cykler av generaliserade egenvektorer
En samling vektorer 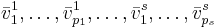 består av s stycken cykler där det övre indexet står för vilken cykel vi är i och det undre står för vilken vektor i cykeln vi är i. En cykel består av generaliserade egenvektorer och hör till ett visst egenvärde λi. Ordet cykel kommer från att
består av s stycken cykler där det övre indexet står för vilken cykel vi är i och det undre står för vilken vektor i cykeln vi är i. En cykel består av generaliserade egenvektorer och hör till ett visst egenvärde λi. Ordet cykel kommer från att 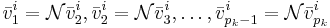 där
där 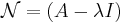 .
.
Anmärkning: En, flera eller alla av cyklerna 1 − s kan höra till ett och samma egenvärde. Det meningsfulla med cykler är att vi i varje cykel får ett Jordanblock med endast ettor i superdiagonalen och kan göra en exakt beskrivning.
Sats 4
Alla cykler av generaliserade egenvektor 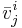 är linjärt oberoende
är linjärt oberoende
Sats 5
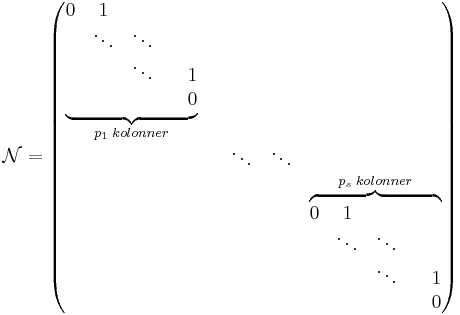
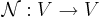 nilpotent matris
nilpotent matris 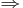 det existerar en bas för V som är en union av cykler av generaliserade egenvektorer, även kallad en strängbas.
det existerar en bas för V som är en union av cykler av generaliserade egenvektorer, även kallad en strängbas.
Sats: Jordans normalform
Varje linjär avbildning 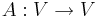 kan representeras av
kan representeras av
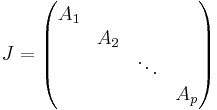 där
där 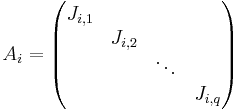 med
med 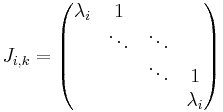
varje Ai kommer från respektive egenvärde λi och delas in i Jordanblock Ji,k, ett för varje cykel som hör ihop med λi. J fås från basbyte A = TJT − 1, där T är en inverterbar matris.
Bevis Jordans Normalform
Beviset är trivialt då vi förstår vad sats 5 betyder. Enligt sats 5 kan varje nilpotent 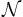 representeras som
representeras som
Med sats 3 som säger att 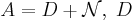 diagonalmatris och
diagonalmatris och 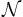 nilpotent matris, kan vi nu skapa Jordans Normalform J med egenvärden i diagonalen och ettor på superdiagonalen från de positioner i N som har ettor.
nilpotent matris, kan vi nu skapa Jordans Normalform J med egenvärden i diagonalen och ettor på superdiagonalen från de positioner i N som har ettor.
Exempel
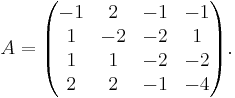
Vi söker den bästa basen till A och det får vi genom att söka egenvärden och egenvektorer till A, precis som vid vanlig diagonalisering. Genom att lösa sekularekvationen fås A:s egenvärden till λ = − 3, − 3, − 3,0. Här har alltså det multipla egenvärdet λ = − 3 algebraisk multiplicitet 3 och det enkla egenvärdet λ = 0 algebraisk multiplicitet 1.
λ1 = 0: ![\bar{v} = t \begin{pmatrix} 1\\1\\0\\1 \end{pmatrix} \Rightarrow E_1=\left[ \begin{pmatrix} 1\\1\\0\\1 \end{pmatrix} \right] , \dim E_1 =](/w/images/sv.rilpedia.org/math/0/4/8/048cc9e98ebafcb14783c7702247c64d.png) algebraisk multiplicitet 1.
algebraisk multiplicitet 1.
λ2 = − 3: ![\bar{v} = t \begin{pmatrix} 1\\-1\\0\\0 \end{pmatrix} +s \begin{pmatrix} 1\\0\\1\\1 \end{pmatrix} \Rightarrow E_2=\left[ \begin{pmatrix} 1\\-1\\0\\0 \end{pmatrix},\begin{pmatrix} 1\\0\\1\\1 \end{pmatrix} \right] , \dim E_2 <](/w/images/sv.rilpedia.org/math/4/2/c/42ce34d658057d4412bcd01947ace1ad.png) algebraisk multiplicitet 3.
algebraisk multiplicitet 3.
Vi ser att A inte är en diagonaliserbar matris. Vi vill nu fylla ut egenrummet för λ = − 3 till ett generaliserat egenrum, detta gör man genom att fylla ut med en generaliserad egenvektor. För att få fram en generaliserad egenvektor löser vi 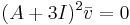 . Detta ger:
. Detta ger:
![\bar{v} = r \begin{pmatrix} 1\\-1\\0\\0 \end{pmatrix} +s \begin{pmatrix} 1\\0\\1\\1 \end{pmatrix} +t \begin{pmatrix} 2\\0\\1\\0 \end{pmatrix} \Rightarrow gen.E_2=\left[ \begin{pmatrix} 1\\-1\\0\\0 \end{pmatrix},\begin{pmatrix} 1\\0\\1\\1 \end{pmatrix},\begin{pmatrix} 2\\0\\1\\0 \end{pmatrix} \right]](/w/images/sv.rilpedia.org/math/a/7/8/a78e9b9c0c928f1474cef892a41a13be.png) dim gen.E2 = 3 = algebraisk multiplicitet.
dim gen.E2 = 3 = algebraisk multiplicitet.
Fördelen med att återanvända vektorer ur E2 är att när vi nu ska skapa en strängbas(Jordan-bas) för att få fram basbytesmatrisen T till jordanformen J så kommer vi börja använda den vektor som ej ligger i egenrummet E2 vilket vi enkelt ser är vektorn 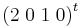
För egenvärdet λ = 0 väljer vi 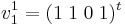 som basvektor i Jordanbasen. Övre siffran i
som basvektor i Jordanbasen. Övre siffran i 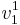 står för vilken cykel vi är i och den undre siffran står för inre numrering i cykeln (Jämför med utseende av Jordanformen J).
står för vilken cykel vi är i och den undre siffran står för inre numrering i cykeln (Jämför med utseende av Jordanformen J).
För egenvärdet λ = − 3 söker vi en strängbas 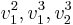 för gen.E2 där
för gen.E2 där 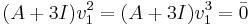 och
och 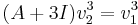
Först väljs 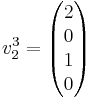 och med denna plockar vi fram
och med denna plockar vi fram 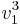 genom samband ovan. Man får då
genom samband ovan. Man får då 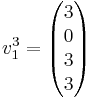
Det som ska gälla för 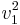 är att denna vektor ska ligga i E2 och vara linjärt oberoende med
är att denna vektor ska ligga i E2 och vara linjärt oberoende med 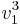 , eftersom
, eftersom 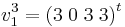 är en av vektorerna i E2 kan man välja den andra som ju är linjärt oberoende med denna, d.v.s.
är en av vektorerna i E2 kan man välja den andra som ju är linjärt oberoende med denna, d.v.s. 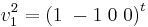
Vi väljer basbytesmatrisen 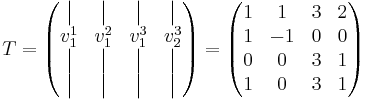
Genom vanligt bassamband fås A = TJT − 1 där J kallas Jordan-formen. Man vet redan i förväg hur denna kommer att se ut, alla egenvärden i diagonalen och ettor i superdiagonalen på de platser man skapat generaliserade egenvektorer. I vårt exempel så blir 
För λ = 0 som var enkelt egenvärde fick vi endast en vanlig egenvektor som fyllde upp E1. För λ = − 3 fick två egenvektorer och en generaliserad egenvektor som vi satte sist i T, därför hamnar 1 i superdiagonalen över den sista 3:an där vi alltså fyllde ut med en generaliserad egenvektor.
Tillämpningar
Det finns ett stort användningsområde för Jordans normalform. Om man ser de diagonaliserbara matriserna som ett specialfall av Jordans normalform så kan man använda samma lösningsgång till att byta till den enklaste möjliga basen.
- System av differentialekvationer
- System av differensekvationer
- Byte till enklare bas för kvadratiska former
Se även
Referenser
- Treil, Sergei. Linear Algebra Done Wrong, 2004, Brown University. Tillgänglig PDF: http://www.math.brown.edu/~treil/index.html