Impulssatsen

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Impulssatsen bygger på Reynolds transportteorem (RTT) och skrivs på integralform:

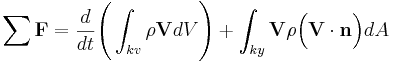
$\sum \mathbf{F} = { d \over dt} \Bigg( \int_{kv} \rho \mathbf{V} dV \Bigg) + \int_{ky} \mathbf{V} \rho \Big( \mathbf{V} \cdot \mathbf{n} \Big) dA$

Där F är en kraftvektor, kv är kontrollvolymen, ky är kontrollytan, V är hastighetsvektorn, ρ är densiteten och n är enhetsvektorn (negativ för inflöde och positiv för utflöde). Impulssatsen kan även skrivas på differentialform (Navier-Stokes ekvationer):

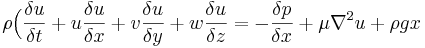
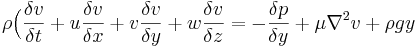
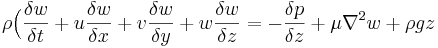
$\rho \Big( {\delta u \over \delta t} + u {\delta u \over \delta x} +v {\delta u \over \delta y} + w {\delta u \over \delta z} = - {\delta p \over \delta x} + \mu \nabla^2 u + \rho g x$ $\rho \Big( {\delta v \over \delta t} + u {\delta v \over \delta x} +v {\delta v \over \delta y} + w {\delta v \over \delta z} = - {\delta p \over \delta y} + \mu \nabla^2 v + \rho g y$ $\rho \Big( {\delta w \over \delta t} + u {\delta w \over \delta x} +v {\delta w \over \delta y} + w {\delta w \over \delta z} = - {\delta p \over \delta z} + \mu \nabla^2 w + \rho g z$

Se även

Denna mekanikartikel är bara påbörjad. Du kan hjälpa till genom att utöka den.

Impulssatsen

Från Rilpedia

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda