Eulers identitet

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Genom att börja vid e0 = 1 och färdas hastigheten i relativt sin position under tidslängden π och addera 1 hamnar man vid 0.

Inom matematisk analys är Eulers identitet, namngiven efter Leonhard Euler, ekvationen:

e^{i \pi} + 1 = 0, \,\!

alternativt

e^{i \pi} = -1, \,\!

där

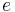e\,\! är Eulers tal, basen för den naturliga logaritmen,
i\,\! är den imaginära enheten
\pi\,\! är pi.

Eftersom talet e är basen för den naturliga logaritmen, så gäller alltid eln(x) = x för alla x > 0. Och eftersom eπi = − 1 så är ln( − 1) = πi. Generellt går detta att skriva som:

\ln(x)=\ln(-x)-\pi i\Leftrightarrow x>0

alternativt

\ln(-x)=\ln(x)+\pi i\Leftrightarrow x>0


Eulers identitet kallas även för Eulers ekvation, men är inte detsamma som Eulers formel. Eulers identitet är ett specialfall av hans formel.

Se även


Lebesgue Icon.svg Denna artikel om matematisk analys är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Eulers_identitet"
Personliga verktyg