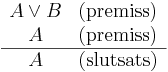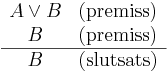Eller-eliminering
Från Rilpedia
| Satslogiska härledningsregler |
|---|
|
Eller-eliminering eller eliminering av disjunktion är en logisk härledningsregel inom satslogiken med formen:
eller
Det vill säga om en av de ingående delarna i satsen "A eller B" är sann så är denna ingående del sann även för sig själv, vilket leder till elimination av disjunktion.
Exempel:
A = "Jag vill ha kaffe"
B = "Jag vill ha te"
A ∨ B (Jag vill ha kaffe eller jag vill ha te)
Jag vill ha kaffe. ; premiss
Slutsats: Jag vill ha kaffe.