Dihedral grupp
Från Rilpedia
Den dihedrala gruppen är ett begrepp inom matematik, den betecknas Dn och avser symmetrigruppen för en regelbunden n-hörning. Elementen i den dihedrala gruppen kan ses som avbildningar från n-hörningen till samma n-hörning, och med den binära operatorn avbildningssammansättning bildar mängden av alla sådana avbildningar en algebraisk struktur som kallas grupp. En dihedral grupp Dn:s ordning är 2n, dvs antalet symmetriavbildningar är totalt 2n stycken.
Grupper är viktiga studieobjekt inom den abstrakta algebran och de dihedrala grupperna är de enklaste exemplen på grupper som inte är abelska grupper, då alla Dn med n > 2 inte är kommutativa.
Exempel: En liksidig triangel
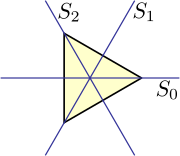
Till exempel är den dihedrala gruppen D3 en abstrakt beskrivning över de sex olika sätt du kan vrida på och spegla hörnen i en liksidig triangel. Man kan vrida triangeln på i princip tre sätt, 0, 120 och 240 grader. Det finns tre symmetrilinjer som man kan använda vid spegling, så gruppen har ordning 6. Om Rk är rotation med  radianer, och Sk är spegling i de olika symmetrilinjerna kan man ställa upp följande Cayleytabell för gruppen:
radianer, och Sk är spegling i de olika symmetrilinjerna kan man ställa upp följande Cayleytabell för gruppen:
| R0 | R1 | R2 | S0 | S1 | S2 | |
|---|---|---|---|---|---|---|
| R0 | R0 | R1 | R2 | S0 | S1 | S2 |
| R1 | R1 | R2 | R0 | S1 | S2 | S0 |
| R2 | R2 | R0 | R1 | S2 | S0 | S1 |
| S0 | S0 | S2 | S1 | R0 | R2 | R1 |
| S1 | S1 | S0 | S2 | R1 | R0 | R2 |
| S2 | S2 | S1 | S0 | R2 | R1 | R0 |
Exempelvis är S0S1 = R2, dvs spegling i symmetrilinje 1 följt av spegling i symmetrilinje 0 är likvärdigt med att rotera triangeln 240 grader.