Differentialekvation

Från Rilpedia

Texten från svenska Wikipedia

Inom matematiken – närmare bestämt inom analysen – är en differentialekvation en ekvation som beskriver förhållandet mellan en okänd funktion och dess derivator. Det är en typ av funktionalekvation.

Innehåll

1 Tillämpningar
2 Begrepp
3 Ett första exempel - Bakterietillväxt
4 Ett andra exempel - Fritt fall
5 Metoder för lösning av differentialekvationer
6 Se även

Tillämpningar

Differentialekvationer används bland annat för att konstruera matematiska modeller av fysikaliska fenomen inom till exempel flödesdynamik eller mekanik. Därför är differentialekvationer ett brett område i både ren och tillämpad matematik. När en matematisk modell av verkligheten görs, innehåller den ofta förändring av en variabel med avseende på en annan variabel. Förändring uttrycks med hjälp av derivator och det är därför den matematiska modellen blir en differentialekvation. För att modellen inte ska bli alltför komplicerad gör man nästan alltid förenklingar av verkligheten.

Differentialekvationer har i sig intressanta egenskaper som huruvida lösningar existerar, och om de gör det - är de unika? Tillämpade matematiker, fysiker och ingenjörer är i allmänhet mer intresserade av hur lösningarna till differentialekvationerna beräknas. Dessa lösningar ligger sedan till grund för formgivning av broar, bilar, flygplan och så vidare. Differentialekvationer är också användbara inom helt andra områden så som framtagandet av ekonomiska modeller.

Begrepp

Antag att $y$ är en funktion av $x$ och

$y', y'',..., y (n)$

betecknar derivatorna

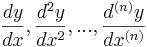
${dy \over dx}, {d^{2}y \over dx^2}, ..., {d^{(n)}y \over dx^{(n)}}$

Ordning

En differentialekvations ordning anger det högsta antalet gånger ( $n$ i exemplet ovan) som någon i ekvationen ingående funktion har deriverats.

Beroende och oberoende variabel

$y$ är den beroende variabeln i differentialekvationen och
$x$ är den oberoende variabeln.

Ordinär och partiell differentialekvation

Ordinära differentialekvationer (ODE) innehåller endast derivata med avseende på en oberoende variabel, som i exemplet ovan.
I partiella differentialekvationer (PDE) är $y$ en funktion av flera variabler, och differentialekvationen innehåller partiella derivator med avseende på mer än en oberoende variabel.

Linjära och ickelinjära ordinära differentialekvationer

Om den ordinära differentialekvationen är linjär är den beroende variabeln $y$ och dess derivata inte multiplar av sig själva. Om den inte är linjär är den icke-linjär.
Exempel:

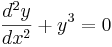
${d^{2}y \over dx^2} + y^3 =0$

är icke-linjär på grund av termen $y 3$ men

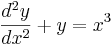
${d^{2}y \over dx^2} + y = x^3$

är linjär på grund av termen $y$ . $x 3$ är den oberoende variabeln och inverkar inte på lineariteten.

Lösningar

Problemet att lösa en differentialekvation består i att finna funktionen $y$ (och indirekt också dess derivator) som uppfyller ekvationen. Till exempel så har differentialekvationen $y'' + y = 0$ allmän lösning $y = A cos x + B sin x$ , där $A$ och $B$ är konstanter som bestäms av randvillkor eller begynnelsevärden.

En differentialekvation har oändligt många lösningar. Däremot finns det teorem som visar att det finns en unik lösning till vissa begynnelsevärdesproblem.

Det finns metoder för att bestämma lösningar till vissa typer av differentialekvationer. I de flesta fall saknas sådana metoder, men alla differentialekvationer kan lösas approximativt med numeriska metoder.

En explicit lösning till en differentialekvation är en funktion av den oberoende variabeln som löser differentialekvationen.
En implicit lösning är ett förhållande mellan den beroende och den oberoende variabeln som indirekt definierar en funktion som är en explicit lösning.

Differentialekvationer då oberoende term saknas

Ett viktigt specialfall är då ekvationerna inte involverar någon oberoende term $x$ . Dessa differentialekvationer kan representeras som vektorfält, och har den viktiga egenskapen att rummet kan delas upp i ekvivalensklasser, där två punkter är ekvivalenta om de ligger på samma lösningskurva. Eftersom fysikens lagar antages vara konstanta över tiden, så styrs den fysiska världen av sådana differentialekvationer. (Se även symplektisk topologi för en abstrakt diskussion.)

Ett första exempel - Bakterietillväxt

Ett typiskt skolexempel som brukar användas för att introducera differentialekvationer är bakterietillväxt i en lösning. Eftersom varje bakterie delar sig med en viss hastighet är bakterietillväxten proportionell mot det totala antalet bakterier vid en given tidpunkt. Om $N$ anger antalet bakterier vid tiden $t$ vet vi därför att

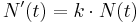
$N'(t) = k \cdot N(t)$

Lösningen till denna differentialekvation är en funktion som har egenskapen att funktionens derivata är proportionell mot funktionen själv. Exponentialfunktionen har precis denna egenskap. Man inser alltså att lösningen måste vara en exponentialfunktion.

Man inser att denna modell av bakterietillväxten bara är approximativ bland annat genom att bakterietillväxten i en lösning så småningom måste avstanna i brist på näring.

Ett andra exempel - Fritt fall

Ett föremål släpps från en viss höjd $h$ och faller på grund av gravitationskraften $F$ . Här görs förenklingarna att gravitationen är den enda kraften som verkar på föremålet, och att gravitationen är konstant. I verkligheten finns också andra krafter, till exempel luftmotstånd.

Newtons andra lag säger att ett föremåls massa $m$ multiplicerat med dess acceleration $a$ är lika med den totala kraften $F$ som verkar på föremålet, eller:

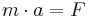
$m \cdot a = F$

Accelerationen är detsamma som derivatan av hastigheten $v$ med avseende på tid $t$ , eller:

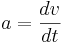
$a = {dv \over dt}$

Hastigheten är i sin tur derivatan av sträckan, eller i detta fall höjden $h$ med avseende på tid $t$ , eller:

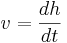
$v = {dh \over dt}$

Alltså är accelerationen andraderivatan av höjden:

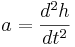
$a = {d^{2}h \over dt^2}$

Den totala kraften $F$ som verkar på föremålet antogs vara endast gravitationen $g$ . Newtons andra lag kan då skrivas som:

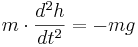
$m \cdot {d^{2}h \over dt^2} = -mg$

(Minustecken eftersom man enligt konvention räknar krafter positiva från jorden.)
Detta är en differentialekvation, som är lätt att lösa med avseende på $h$ . Först divideras med $m$ , vilket ger

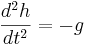
${d^{2}h \over dt^2} = -g$

Integrering av båda leden ger

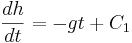
${dh \over dt} = -gt + C_1$

och ytterligare en integrering ger

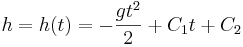
$h = h(t) = -{gt^2 \over 2} + C_{1}t + C_2$

Integrationskonstanterna $C 1$ och $C 2$ kan bestämmas om man vet föremålets begynnelsehöjd och begynnelsehastighet.
Resultatet är nu en funktion, eller en formel, för föremålets höjd vid tiden $t$ .

Metoder för lösning av differentialekvationer

Vissa differentialekvationer kan lösas analytiskt, och lösningen blir då exakt. I analytiska lösningar kan man använda transformation, oftast Laplacetransformation för ordinära differentialekvationer och Fouriertransformation för partiella.

För de flesta differentialekvationer behövs numeriska metoder. Några vanliga numeriska metoder för lösning av differentialekvationer är Eulers metod och Runge-Kuttas metod för begynnelsevärdesproblem, och provskottsmetoden för randvärdesproblem. Partiella differentialekvationer är särskilt känsliga för fel i lösningen.

Se även

Differentialekvation

Från Rilpedia

Innehåll

Tillämpningar

Begrepp

Ordning

Beroende och oberoende variabel

Ordinär och partiell differentialekvation

Linjära och ickelinjära ordinära differentialekvationer

Lösningar

Differentialekvationer då oberoende term saknas

Ett första exempel - Bakterietillväxt

Ett andra exempel - Fritt fall

Metoder för lösning av differentialekvationer

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk